Radically Rooted Reciprocals
⎣ ⎡ ( 3 1 ) − 3 4 ⎦ ⎤ 2 9 × 9 − 3 = ?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
Yeah my answer is true...yahh
https://brilliant.org/discussions/thread/determinants/ proove this one please 😍
Great steps. My steps are actually similar to yours.
Log in to reply
No wonder it is good.
Log in to reply
You should check out and try to solve some of the problems that I have posted on my account right here.
(1/3)= 3^(-1)
(((3^-1)^-4/3)^9/2) x (3^2)^-3
3^(-1 * -4/3 * 9/2) x 3^(2 * -3)
(3^6) * (3^(-6))
(3^6)/(3^6) = 1
Very nice explanation!
Yeah my answer is true...yooooo
(-4/3)(9/2)=-6 ((1/3)^-6)*(9^-3)=(9^-3)/(3^-6)=(3^6)/(9^3)=729/729=1
First, look at the ranks. I saw two ranks between brackets. So I calculate -4/3 times 9/2 equals to -6. Then, change 1/3 into rank form, that is equals to 3 rank minus one, so I used -1 to be timed with -6, I got 6. So now I have 3 rank 6. 3 rank 6 is equal to 729. Now what's with 9 rank minus 3? Yeah, change it into fraction form, that is equals to one per 9 rank 3. Why no minus? Because it goes inside denominator side. 9 rank 3 is equal to 729, so 9 rank minus 3 is equals to one per 729. I have a same numerator and denominator number, so it goes 729/729, you got 1. The answer is 1.
Use John's Derirative Binomial Expansion Theorem.
Moderator note:
How?
=[3^(4/3)]^9/2x(3^-6) =3^[(4/3)x(9/2)]x(3^-6) =(3^6)(3^-6) =3^0 =1
Consider ((1/3)^-4/3)^9/2 => (1/3)^-4/3 * 9/2 => (1/3)^-4/2 * 9/3 => (1/3)^-6 => (3)^6 * 9^-3 => (3^2)^3 * 9^-3 => 9^3 * 9^-3 => 9^(3-3) => 9^0 = 1
[(1/3)^-4/3]^9/2 term in the expression can be rewritten as [(1/3)^[(-4/3)X(2/3)]], which simplifies to [(1/3)^-6], which then can be rewritten as 3^6. The 9^-3 term can be rewritten as (3^2)^-3 which simplifies to 3^-6. Therefore, (3^6)X(3^-6)=[3^(6-6)]=3^0=1
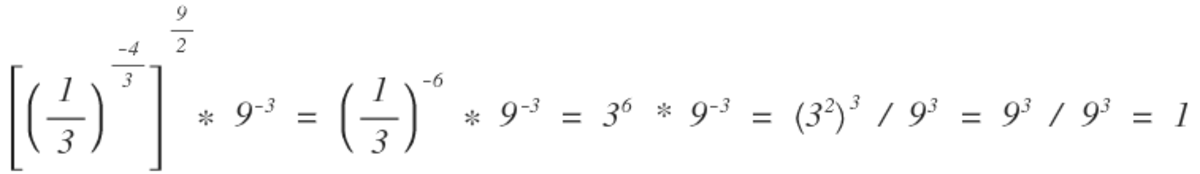
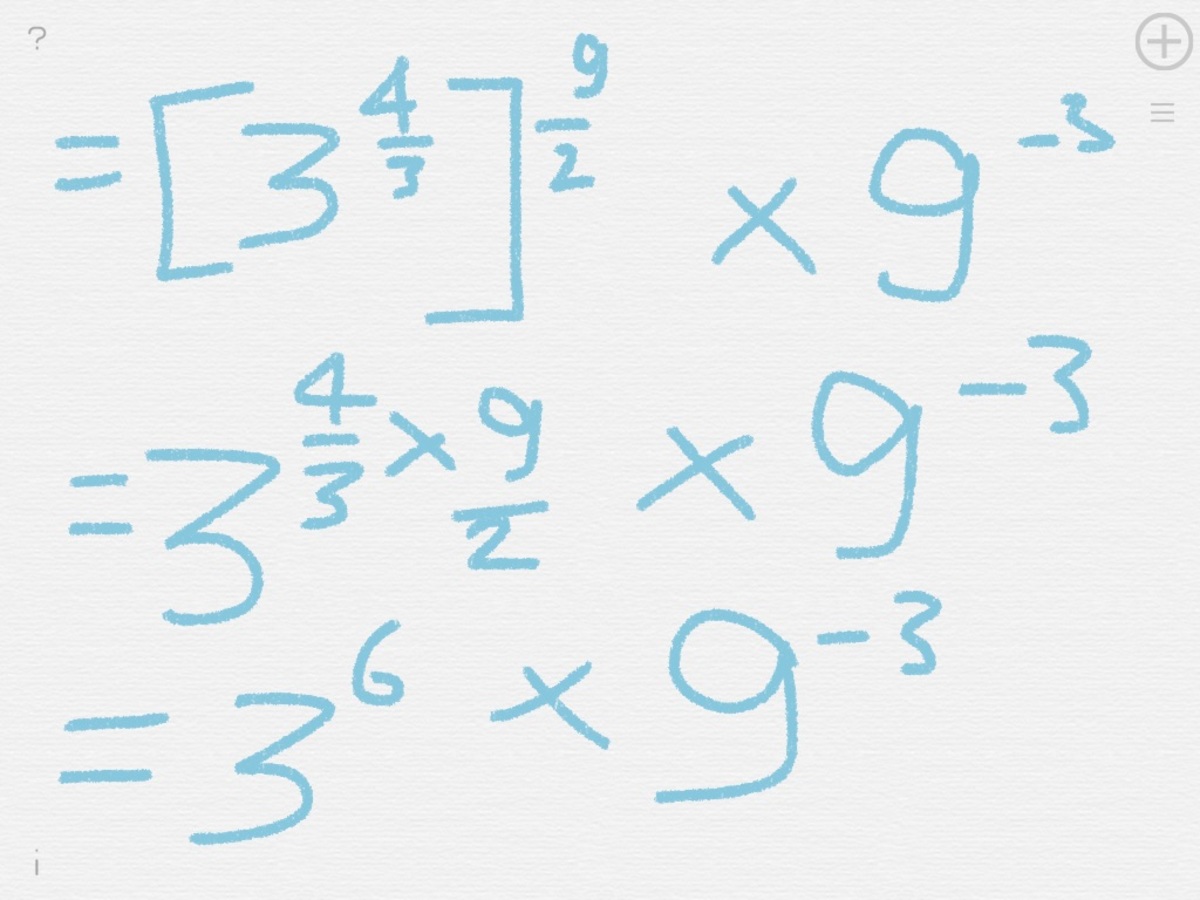
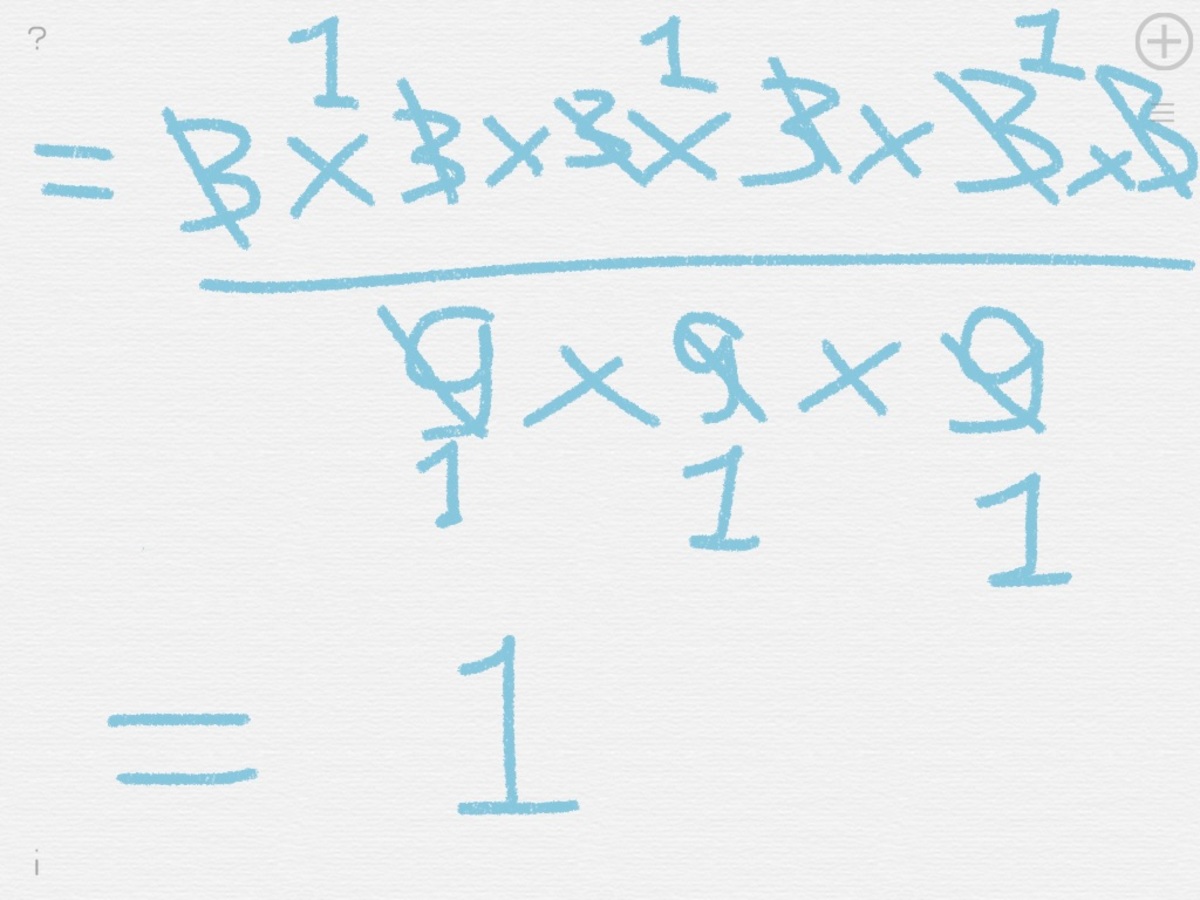
[ ( 3 1 ) − 3 4 ] 2 9 ( 9 − 3 ) = [ ( 3 − 1 ) − 3 4 ] 2 9 ( ( 3 2 ) − 3 ) = ( 3 3 4 ) 2 9 ( 3 − 6 ) = ( 3 3 4 × 2 9 ) ( 3 − 6 ) = ( 3 6 ) ( 3 − 6 ) = 3 6 − 6 = 3 0 = 1