Rational height of a Triangle inside a Triangle

Geometry Level 4

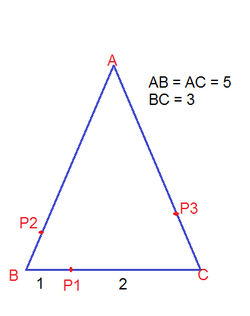Diagram above is not to scale:

Let ABC be a given triangle with AB = AC = 5 and BC = 3, a point P1 is on BC such that BP1 = 1.

Points P2 and P3 are chosen on sides AB, AC respectively such that they are at the shortest distance from P1.

Find the height of the triangle P1P2P3, with respect to the base P2, P3.

While I was not interested in a irrational solution, the best i could do was to express the height as follows

$h = \frac{ a*b} { (c^d) *d * \sqrt{e} }$

where a, b, c, d, e are distinct prime integers,

find a + b + c + d + e ?

Source: Own work.

The answer is 50.

2 solutions

Abdelrahman Sabri
Sep 15, 2014

First , I get an expression for P1P2 in one variable ( F(x) ) by Pythagoras theorem, F'(x)=0 to get the shortest length of P1P2. And I do so for P1P3. Then I can find P3C , P2B , AP2 and AP3, using the angle BCA and AP2 and AP3 I get P2P3 by the cosine rule, then I get the angle P1P3P2 by the cosine rule, then I get the required height by the sine rule.

Is there a shorter solution ? .... I feel that this solution is too long

Unstable Chickoy
Jun 11, 2014

height is

$h = \frac{13\times 7}{5^2 \times 2\times \sqrt{23}}$

$a + b +c + d + e = 13 + 7 + 5 + 2 +23 = \boxed{50}$

nice problem. I had a lengthy solution.

Unstable Chickoy - 7 years ago

I found the cosines of all the $\triangle ABC$ angles and then all the sides of the $\triangle P_1P_2P_3$ and hence by using the formula $h=\frac{2S_{\triangle P_1P_2P_3}}{P_2P_3}$ with the help of the Heron's formula got the height. Did you do this the same way?

mathh mathh - 6 years, 9 months ago

Oh yeah, I also did it by the same method.

Alan Enrique Ontiveros Salazar - 6 years, 9 months ago

Rational height of a Triangle inside a Triangle

The answer is 50.

2 solutions

0 pending reports