Ratios!!
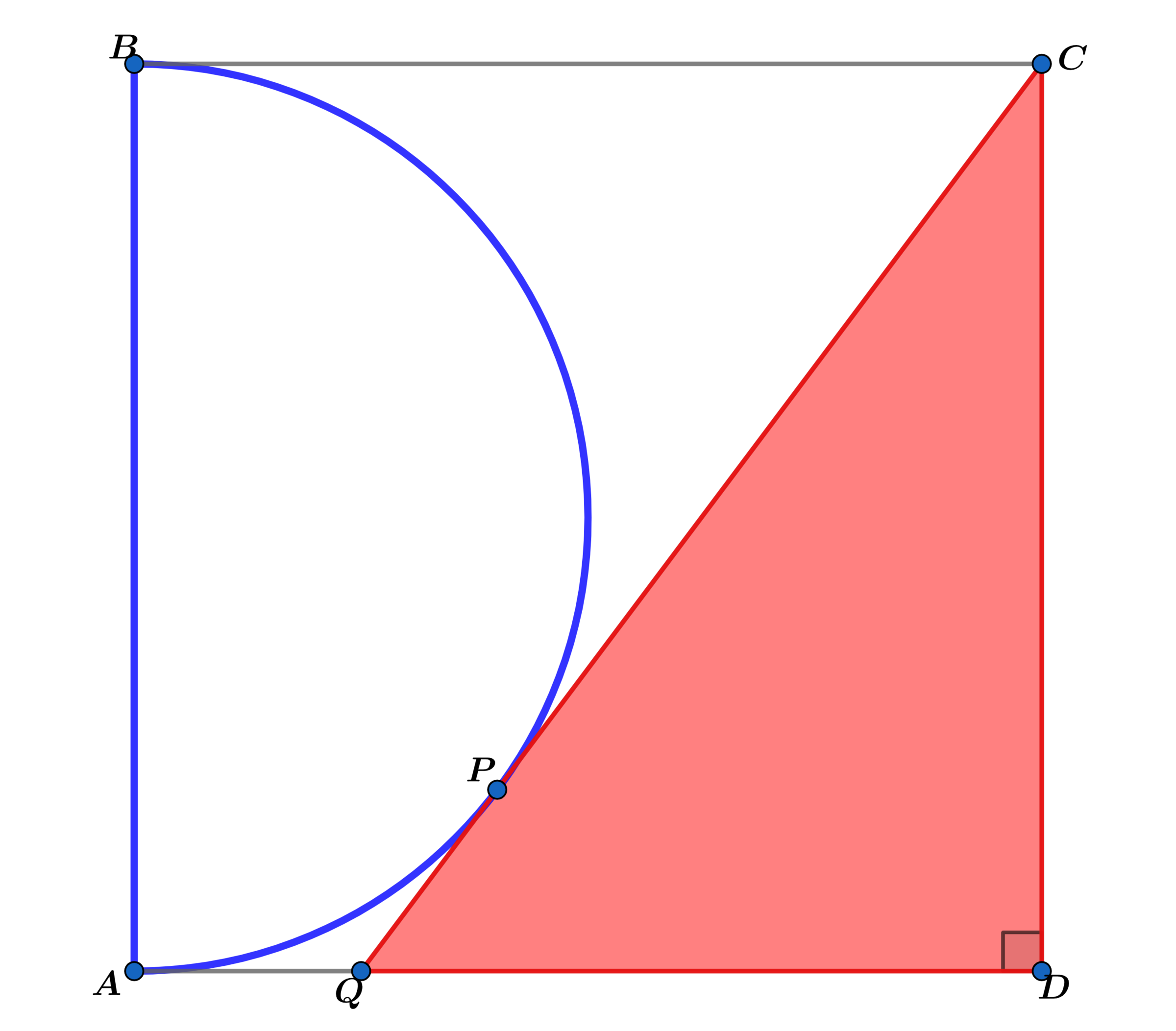
In square A B C D , C Q is tangent to the semicircle at P .
If A A B C D A △ Q C D = β α , where α and β are coprime positive integers, find α + β .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Solution 1:
Without loss of generality, let the side of the square be 1 . Also let O be the center of the semicircle and draw in O C and O P :
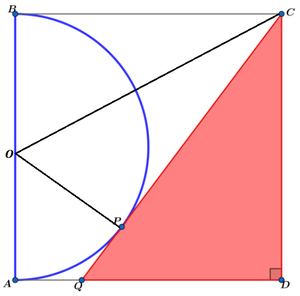
Since ∠ O B C = ∠ O P C = 9 0 ° , O B = O P = 2 1 , and O C = O C , △ O B C ≅ △ O P C by HL congruence, so ∠ B C O = ∠ P C O by corresponding parts.
Let α = ∠ B C O = ∠ P C O , β = ∠ Q C D , and b = Q D . From △ O B C , tan α = 1 2 1 = 2 1 , and from △ Q C D , tan β = 1 b = b .
By the angle sum of ∠ B C D , 2 α + β = 9 0 ° . Substituting tan α = 2 1 and tan β = b and then dividing by 2 gives tan − 1 2 1 + 2 1 tan − 1 b = 4 5 ° .
Letting T = tan ( 2 1 tan − 1 b ) , then tan ( tan − 1 2 1 + tan − 1 T ) = tan 4 5 ° , or applying the tangent sum equation, 1 − 2 1 T 2 1 + T = 1 , which solves to T = 3 1 .
Therefore, b = tan ( 2 tan − 1 T ) = 1 − T 2 2 T = 1 − ( 3 1 ) 2 2 ⋅ 3 1 = 4 3 , so that A A B C D A △ Q C D = 1 2 2 1 ⋅ 4 3 ⋅ 1 = 8 3 , which means α = 3 , β = 8 , and α + β = 1 1 .
Solution 2:
Without loss of generality, let A B = B C = C D = A D = 1 , and place the whole diagram on a coordinate graph so that A is at ( 0 , 0 ) and C is at ( 1 , 1 ) .
The equation of the semicircle is then x 2 + ( y − 2 1 ) 2 = 4 1 , and the equation of the line C Q with slope m is y = m ( x − 1 ) + 1 .
Substituting y = m ( x − 1 ) + 1 into x 2 + ( y − 2 1 ) 2 = 4 1 and solving for x gives ( m 2 + 1 ) x 2 + ( m − 2 m 2 ) x + ( m 2 − m ) = 0 .
For a tangent line, the discriminant of x will be 0 , so ( m − 2 m 2 ) 2 − 4 ( m 2 + 1 ) ( m 2 − m ) = − m ( 3 m − 4 ) = 0 , which solves to m = 3 4 for m > 0 .
The equation of the line C Q is then y = 3 4 ( x − 1 ) + 1 , which solving 0 = 3 4 ( x − 1 ) + 1 gives an x -intercept of x = 4 1 = A Q .
Therefore, Q D = 1 − A Q = 1 − 4 1 = 4 3 , so that A A B C D A △ Q C D = 1 2 2 1 ⋅ 4 3 ⋅ 1 = 8 3 , which means α = 3 , β = 8 , and α + β = 1 1 .
O C = 2 5 s ⟹ P C = s
and
a 2 + ( b − 2 s ) 2 = 4 s 2
( a − s ) 2 + ( b − s ) 2 = s 2
⟹
a 2 + b 2 − b s = 0
− 1 ∣ ( a 2 + b 2 − 2 b s − 2 a s = − s 2 )
⟹ b + 2 a = s ⟹ b = s − 2 a ⟹ a ( 5 a − 2 s ) = 0 and a = 0 ⟹ a = 5 2 s ⟹ b = 5 s ⟹
P ( 5 2 s , 5 s ) and C ( s , s ) ⟹ m P C = 3 4 ⟹ y − s = 3 4 ( x − s ) and y = 0 ⟹
x = 4 s ⟹ Q D = 4 3 s ⟹ A △ Q C D = 8 3 s 2 ⟹
A A B C D A △ Q C D = 8 3 = β α ⟹ α + β = 1 1 .