Rawan's Strange Clock
Rawan has a strange clock as the hours' hand is moving with its normal speed and direction, but the minutes' hand is moving with its normal speed but the opposite direction (moving counterclockwise).
How many times Rawan's clock hands will be overlapping in 36 hrs?
Note: hands will be over lapping when the angle between them is 0, just like when the time is 12:00.
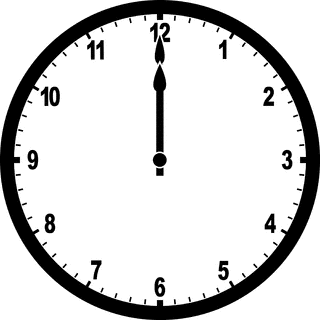
The answer is 39.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Lets say a full hand rotation is 3 6 0 degrees..
The hours hand will move 3 6 0 / 1 2 = 3 0 deg in hr
The minutes hand will move 3 6 0 deg in hr
The relative speed between them is ( 3 6 0 + 3 0 ) = 3 9 0 deg in hr .. (as they moves toward each other).
To calculate the overlapping interval, t = 3 9 0 3 6 0 = 3 9 3 6 hr
No. of overlapping times = 3 6 / 3 9 3 6 = 3 9