RC circuit
In the circuit shown, switch S is closed at time 0, then the charge on the capacitor C 2 in steady state in μ C .
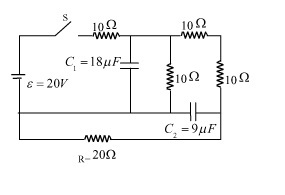
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
In the steady state we know that any current that pass through capacitor is equal to zero.
So, we reduce our problem from DE to simple linear equation. We have
2 = 2 i 1 + i 2
2 = i 1 + 5 i 2
From this we have i 2 = 9 2 A
then we got Q = 9 ∗ 9 4 0 = 4 0 μ C
Another extremely overrated problem..
what do you mean by i 1 & i 2 ?
At steady state, no current passes through the capacitors. For ease, we can just remove them from the circuit. After distributing the current with help of Kirchhoff's laws, the circuit is like the one above. It is clear that the potential across the points A and B is the potential across the capacitor C 2 .
V A + 1 0 ( 9 8 ) − 1 0 ( 9 1 0 ) − 1 0 ( 9 2 ) = V B V A − V B = 9 4 0 Q = 9 ( 9 4 0 ) = 4 0 μ C