RC Low-Pass Filter - RMS Attenuation

Electricity and Magnetism Level 3

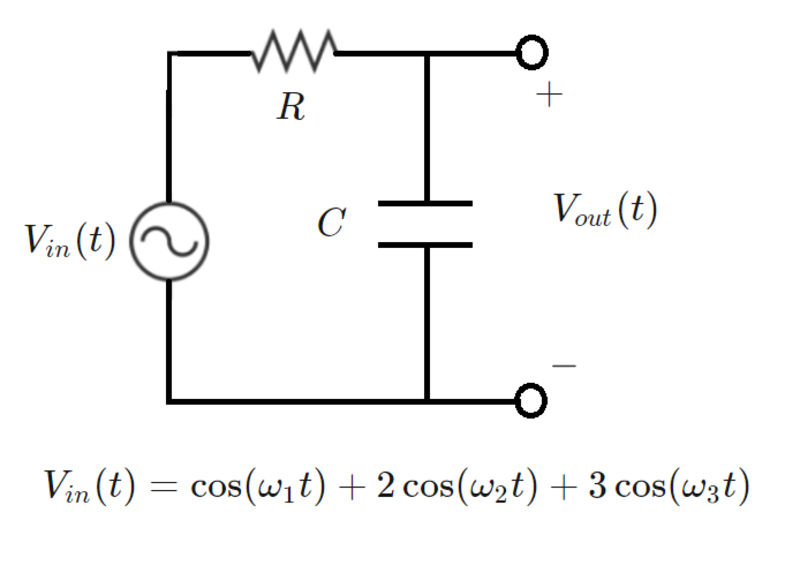
The circuit below is an RC low-pass filter with a voltage input consisting of sinusoids at several different frequencies. The filter cutoff frequency is $f_c$ (see details below).

In steady-state, what is the ratio of the RMS output voltage to the RMS input voltage?

Note: This can be solved two different ways. Both methods yield the same result.

The first way involves a superposition of three different AC steady states - one for each frequency. And then the RMS voltage is the square root of the sum of the squares of the individual voltage magnitudes at each frequency. $V_{RMS} = \sqrt{{|V|_1}^2 + {|V|_2}^2 + {|V|_3}^2}$
The second way involves a time-domain simulation to calculate the composite capacitor voltage, as well as the calculation of the following integral: $V_{RMS} = \sqrt{\frac{1}{T} \int_0^T v^2(t) \, dt}$ . Note that here, $T$ must be an integer multiple of each of the constituent signal periods.

Details and Assumptions:

$R = 1$
$(f_1,f_2,f_3,f_c) = (60,120,180,90)$ .
$(\omega_1, \omega_2, \omega_3, \omega_c) = (2 \pi f_1, 2 \pi f_2, 2 \pi f_3, 2 \pi f_c )$
$\large{C = \frac{1}{R \, \omega_c}}$

The answer is 0.53.

1 solution

Karan Chatrath
Sep 5, 2019

General Outline of Solution

This circuit is analysed in steady-state by applying the principle of superposition.

Consider the voltage component:

$V_{i1} = \cos(\omega_1t)$ The impedance of the circuit considering only this input is:

$Z_1 = R + \frac{1}{j\omega_1C}$

Here $j = \sqrt{-1}$ . The current is then:

$I_1 = \frac{V_{i1,max}}{Z_1}$

The voltage drop across the capacitor is then:

$V_{o1} = I_1\left( \frac{1}{j\omega_1C}\right)$

This same process is repeated for the other two voltage input components which are:

$V_{i2} = 2\cos(\omega_2t)$ $V_{i3} = 3\cos(\omega_3t)$

Finally, we obtain output voltages $V_{o1}$ , $V_{o2}$ , $V_{o3}$ , which are complex numbers.

The required answer is then:

$\boxed{A = \frac{\sqrt{\mid V_{o1}\mid^2 + \mid V_{o2}\mid^2 + \mid V_{o3}\mid^2}}{\sqrt{\mid V_{i1,max} \mid^2 + \mid V_{i2,max} \mid^2 + \mid V_{i3,max} \mid^2}}=0.53}$

Solution verified by solving the system differential equation numerically and computing the required ratio by evaluating the required integrals, again numerically. A closed-form solution is possible but tedious.

RC Low-Pass Filter - RMS Attenuation

The answer is 0.53.

1 solution

0 pending reports