Re : Last two digits

Since $3 \equiv -1 \pmod{4}$ , it follows that $3^2 \equiv 1 \pmod{4}$ and hence that $3^{400} \equiv 1 \pmod{4}$ . Also $3^4 \equiv 1 \pmod{5}$ , and hence $3^{20} \equiv 1 \pmod{25}$ , so that $3^{400} \equiv 1 \pmod{25}$ . Putting these congruences together we deduce that $3^{400} \equiv 1 \pmod{100}$ , making the answer $\boxed{01}$ .

By Binomial Expansion

$\begin{aligned} 3^{400} & \equiv 9^{200} \text{ (mod 100)} \\ & \equiv (10-1)^{200} \text{ (mod 100)} \\ & \equiv (10^{200}-200\cdot 10^{199}+\cdots - 200\cdot 10 + 1) \text{ (mod 100)} \\ & \equiv 1 \text{ (mod 100)} \end{aligned}$

Therefore, the last two digits of $3^{400}$ is $\boxed{01}$ .

---

By Euler's Theorem

We need to find $3^{400} \bmod 100$ . Since 3 and 100 are coprime integers, that is $\gcd(3,100)=1$ , we can apply Euler's theorem as follows. Note that the Euler's totient function $\phi(100) = 100 \times \frac 12 \times \frac 45 = 40$ .

$\begin{aligned} 3^{400} & \equiv 3^{400 \bmod \phi(100)} \text{ (mod 100)} \\ & \equiv 3^{400 \bmod 40} \text{ (mod 100)} \\ & \equiv 3^0 \text{ (mod 100)} \\ & \equiv 1 \text{ (mod 100)} \end{aligned}$

Therefore, the last two digits of $3^{400}$ is $\boxed{01}$ .

Use Euler's theorem

$400 \equiv 0 \ mod \ \phi(100)=40 \implies 3^{400} \equiv 3^0 \equiv 1 \ mod \ 100$

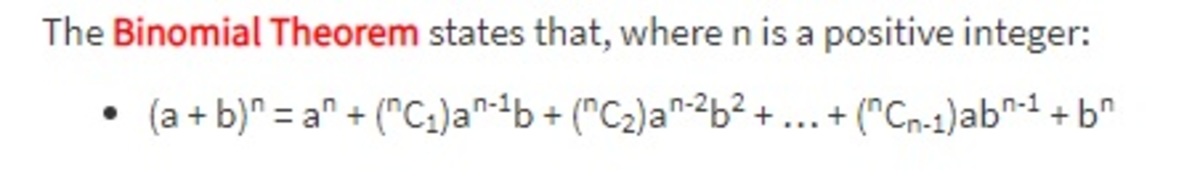
3^400 = (3^4)^100 = ( 1 + 80) ^ 100

Expanding (1 + 80) ^ 100 using the binomial theorm

The first few terms are 1 + 100 * 80 + 4450 * 6400 + 161700*512000 + ....

= 8001 + 4450 6400 + 161700 512000 + ....

The last few digits of the third and the fourth terms are 000, 00000. So if the first two terms are added to the other terms, the last two digits will remain

the same as one where the first and the second terms are added ( 01). So the last two digits of 3^400 are 01 , answer choice A.

Youtube Tutorial :

Last two digits of 3^400

Verified using Excel :

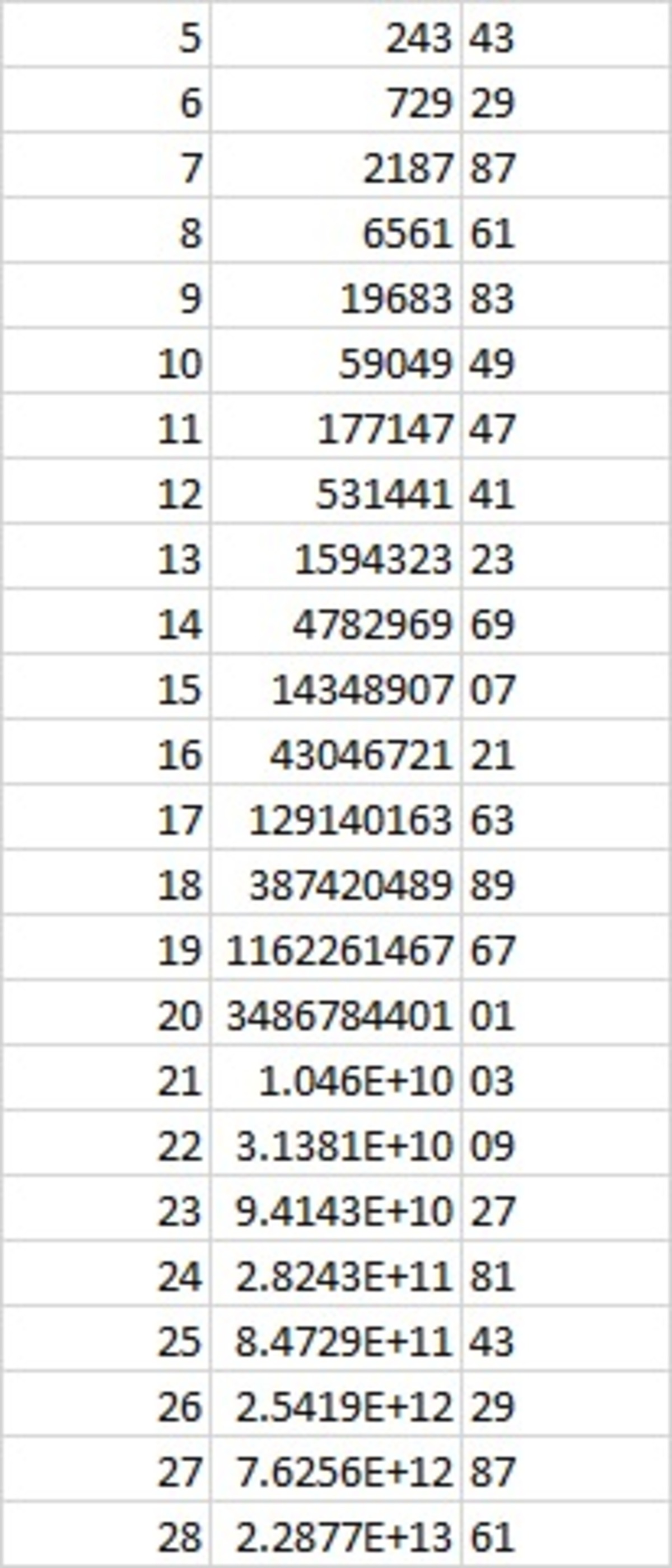
The last two digits of 3^x cycles with a period of 20 powers. So the last two digits of 3^400 = last two digits of 3^20 which is equal to 01.