Reach for the Summit - M-S5-A1
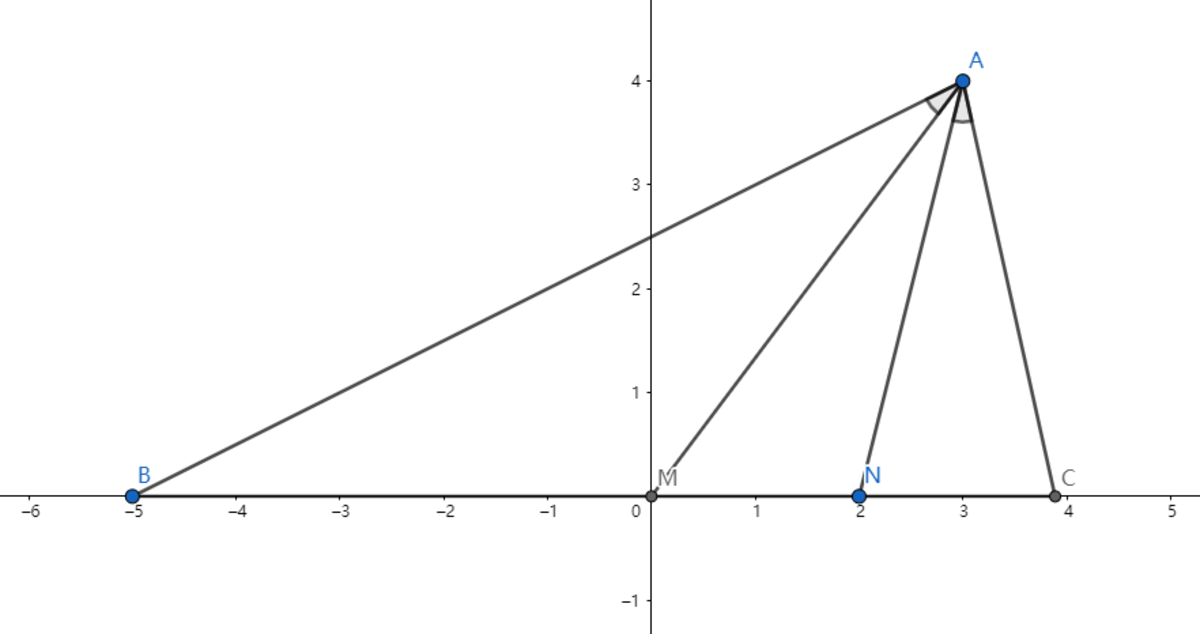
In △ A B C , A ( 3 , 4 ) , B ( − 5 , 0 ) , M ( 0 , 0 ) , N ( 2 , 0 ) , C is a point on the positive x -axis such that ∠ B A M = ∠ C A N .
If the circumcenters of △ A M N and △ A B C are D ( x 1 , y 1 ) and E ( x 2 , y 2 ) respectively, find ⌊ 1 0 0 0 ( x 1 + 2 y 1 + 3 x 2 + 4 y 2 ) ⌋ .
Hint: Find the relationship of A D and A E .
The answer is 8527.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
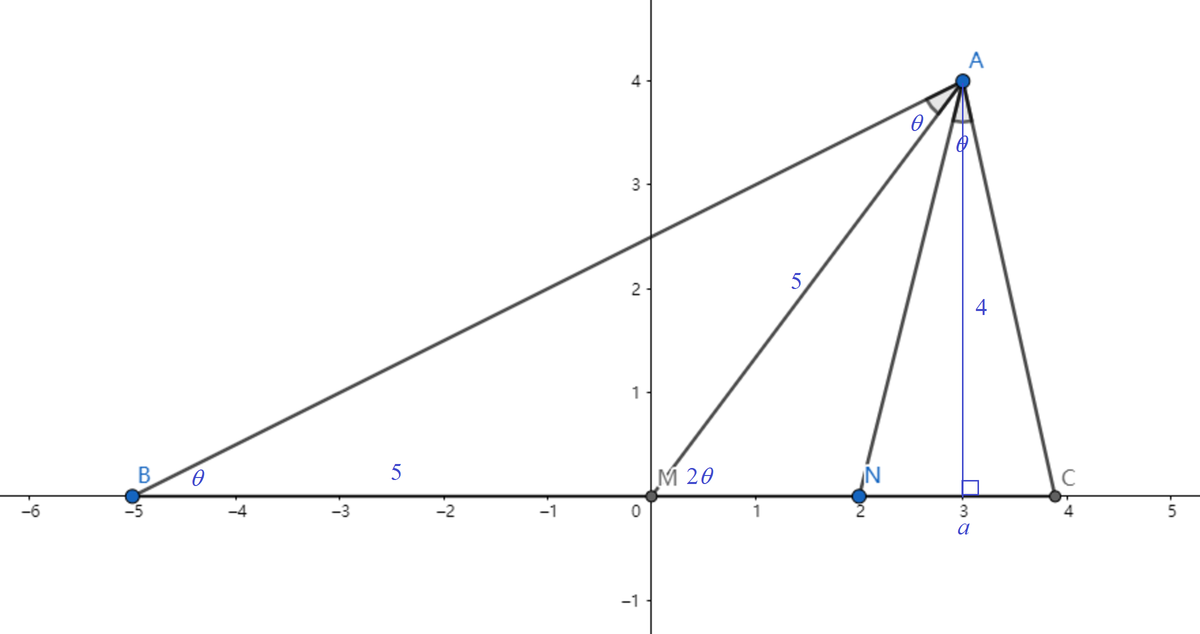
Since A ( 3 , 4 ) , we note that A M = 5 . As B M = A M = 5 , △ A M B is isosceles and ∠ A B M = ∠ B A M = ∠ C A N = θ . We also note that △ A B C and △ C A N are similar. Then we have:
N C A C = A N A B = A C B C
Then N C A C = A N A B = 1 2 + 4 2 8 2 + 4 2 = 1 7 8 0 . Let N C = a ; then A C = 1 7 8 0 a . And also:
A C B C B C 7 + a 1 1 9 + 1 7 a ⟹ a = A N A B = A N A B × A C = 1 7 8 0 × 1 7 8 0 a = 1 7 8 0 a = 8 0 a = 6 3 1 1 9
We can find the coordinates of circumcenter by first finding the circumradius using the formula 2 r = sin A a , where a is the side length opposite ∠ A in a triangle.
For △ A M N , r 1 = 2 sin ∠ A M N A N = 2 × 5 4 1 7 = 8 5 1 7 . Noting that x 1 is the midpoint of M N or x 1 = 1 , then
x 1 2 + y 1 2 1 2 + y 1 2 ⟹ y 1 = r 1 2 = 6 4 2 5 × 1 7 = 8 1 9
Similarly for △ A B C , r 2 = 2 sin ∠ A B C A C = 2 × 5 1 1 7 8 0 × 6 3 1 1 9 = 9 1 0 1 7 . x 2 = 2 − 5 + 2 + a = − 9 5 , and y 2 = ( 9 1 0 1 7 ) 2 − ( − 9 5 + 5 ) 2 = 9 1 0 .
Therefore ⌊ 1 0 6 ( x 1 + 2 y 1 + 3 x 2 + 4 y 2 ) ⌋ = 8 5 2 7 .
Position coordinates of C are ( 9 3 5 , 0 )
Equation of perpendicular bisector of M N is x = 1 , of A M is
y − 2 = − 4 3 ( x − 2 3 )
Solving we get the position coordinates of the circumcentre of △ A M N as ( 1 , 8 1 9 )
Equation of perpendicular bisector of B C is x = − 9 5 ,
of A B is y − 2 = − 2 ( x + 1 )
Solving we get the position coordinates of the circumcentre of △ A B C as
( − 9 5 , 9 1 0 )
So, x 1 = 1 , y 1 = 8 1 9 , x 2 = − 9 5 , y 2 = 9 1 0
Hence the required answer is 8 5 2 7 .