Reach for the Summit - M-S5-A2
Find the smallest and largest inscribed equilateral triangle in an 1 × 1 square.
If the smallest triangle has area S m i n and the largest has area S m a x , submit
⌊ 1 0 6 ( S m a x − S m i n ) ⌋
The answer is 31088.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
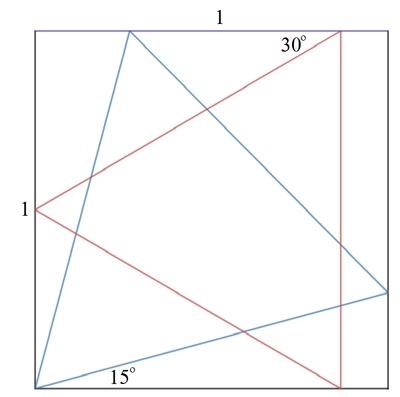
The largest equilateral triangle one that is symmetrical about the diagonal of the square as indicated by the blue triangle. The smallest equilateral triangle is one that is symmetrical about the line joining the midpoints of two opposite sides with a vertex at the midpoint of a side as indicated by the red triangle.
The largest triangle has a side of a m a x = cos 1 5 ∘ 1 and hence an area of S m a x = 2 a m a x 2 sin 6 0 ∘ = 2 cos 2 1 5 ∘ sin 6 0 ∘ = 1 + cos 3 0 ∘ sin 6 0 ∘ = 2 + 3 3 .
The smallest triangle has a side of a m i n = sin 3 0 ∘ 2 1 = 1 and hence an area of S m i n = 2 a m i n 2 sin 6 0 ∘ = 4 3 .
Therefore, ⌊ 1 0 6 ( S m a x − S m i n ) ⌋ = ⌊ 1 0 6 ( 2 + 3 3 − 4 3 ) ⌋ = 3 1 0 8 8 .
Where's the proof that your configurations are the ones that really optimize the inscribed triangle?
Log in to reply
I don't have.
Log in to reply
I have added a solution. Please check whether my proof is correct.
Setup
We want to find configurations that maximize or minimize the difference between the area of a square and the area of an equilateral triangle inscribed in it. To find these configurations, we will take the following approach.
We will take an equilateral triangle of side length d . Then, we will try to fit squares around it. Our goal will be to find the largest and the smallest fitting squares.
To that end, we will hinge one vertex (namely, A ) of the equilateral triangle at the origin. Other vertices ( B , C ) of the triangle will me movable. The x-axis will contain the bottom side of the fitting square, and this bottom side will have a vertex, which is at origin, on it. The top side will be parallel to the x-axis. The left and the right side of the square will be parallel to the y-axis, and will contain at least one vertex each.
Case 1
The enclosing square here is named A P Q R . Let a denote the side length of the square. Also let ∠ B A P = k . So, ∠ C A P = 3 π + k .
In this case, k will vary from 0 to 6 π .
From the triangle Δ A B P , cos k = A B A P ⟹ a = A P = A B cos k = d cos k
But this square will not always circumscribe Δ A B C because the vertex C needs to be on Q R . This condition can be expressed as a = d cos k = A C sin ( 3 π + k ) = d sin ( 3 π + k ) ⟹ sin ( 2 π − k ) = sin ( 3 π + k ) ⟹ ( 2 π − k ) = ( 3 π + k ) ∴ k = 1 2 π
Therefore, there is only one valid value of k for 0 ≤ k < 6 π . And the corresponding side length is a 1 = d cos ( 1 2 π )
Case 2
The enclosing square here is J K L M . The side length is denoted by a as before. Let ∠ B A K = k and ∠ C A K = 3 π + k .
In this case, k will vary from 6 π to 3 π . Now we will get an expression for the side length. a = J K = A K + J A = d cos k − d cos ( 3 π + k ) a = 2 d sin ( 6 π ) sin ( 6 π + k ) ∴ a = d sin ( 6 π + k )
We notice that the a needs to clear the height of A C . Otherwise, L M will enter inside Δ A B C . So, a ≥ A C sin ( 3 π + k ) d sin ( 6 π + k ) ≥ d sin ( 3 π + k ) 6 π + k ≥ π − 3 π − k ∴ k ≥ 4 π
So, the valid values of k lies on the range [ 4 π , 3 π ] . Also, a = sin ( 6 π + k ) is an increasing function for k ∈ [ 4 π , 3 π ] . Hence, the extrema are a 2 = d sin ( 6 π + 4 π ) = d sin ( 1 2 5 π ) a 3 = d sin ( 6 π + 3 π ) = d sin ( 2 π ) = d
Other cases
All the configurations of other values of k are just mirror images of the two cases mentioned above. So, we have effectively found all the optimum configurations.
Results
We notice that a m i n = a 1 = d cos ( 1 2 π ) = d sin ( 1 2 5 π ) = a 2 ⟹ a m i n = d sin ( 1 2 5 π ) a m a x = d
In our case, the reverse is happening: the square is of fixed length, and the triangle length is variable. Hence, d m i n = a = 1 d m a x = sin ( 1 2 5 π ) a = csc ( 1 2 5 π )
Therefore, ⌊ 1 0 6 ( S m a x − S m i n ) ⌋ = ⌊ 1 0 6 4 3 ( csc 2 1 2 5 π − 1 ) ⌋ = 3 1 0 8 8
P.S. If you want to play with the setup, feel free to use my Desmos project .