Reach for the Summit - M-S6-A2
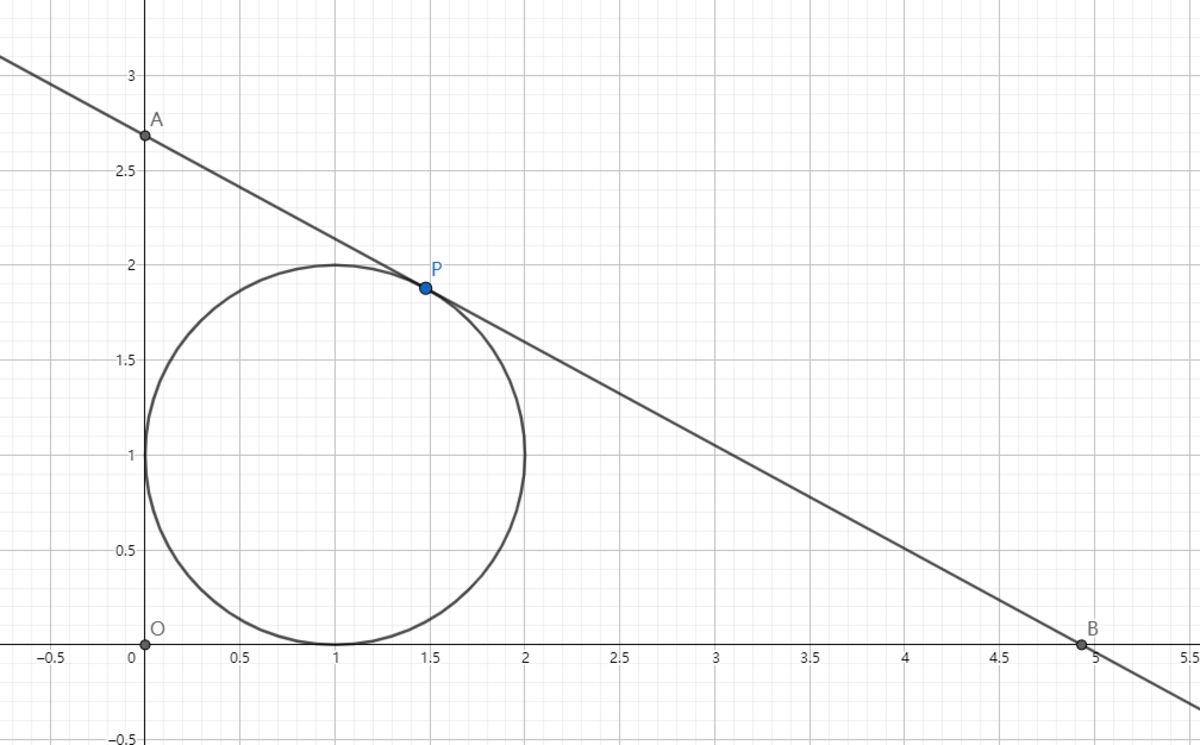
As shown above, line l is tangent to curve C : x 2 + y 2 − 2 x − 2 y + 1 = 0 and it intersects with y-axis at point A , x-axis at point B , O is the origin, ∣ O A ∣ > 2 , ∣ O B ∣ > 2 . Then find the minimum area for △ A O B .
Let S denote the minimum area. Submit ⌊ 1 0 0 0 S ⌋ .
The answer is 5828.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The area of △ O A B will be minimum when ∣ O A ∣ = ∣ O B ∣ = 2 + 2
The minimum area will be
2 1 × ( 2 + 2 ) 2 = 3 + 2 2 ≈ 5 . 8 2 8 4 2 7
Hence the required answer is 5 8 2 8 .
Note that C : x 2 + y 2 − 2 x − 2 y + 1 = 0 ⟹ C : ( x − 1 ) 2 + ( y − 1 ) 2 = 1 is the incircle of △ A O B with center at ( 1 , 1 ) and radius 1 . Then the △ A O B with the smallest area is when it is an isosceles triangle with O A = O B and ∠ A = ∠ B = 4 5 ∘ (see proof below):
Then we have O A = O B = 2 ( 1 + 2 ) and the minimum area of △ A O B , S = 2 O A 2 = ( 1 + 2 ) 2 = 3 + 2 2 ≈ 5 . 8 2 8 ⟹ ⌊ 1 0 0 0 S ⌋ = 5 8 2 8 .
Proof
Let O B = a , O A = b , and ∠ O B A = θ . Then we have:
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ a = cot ( 2 θ ) + 1 b = cot ( 4 5 ∘ − 2 θ ) + 1 Let t = tan 2 θ ⟹ ⎩ ⎪ ⎨ ⎪ ⎧ a = t 1 + 1 = t 1 + t b = 1 − t 1 + t + 1 = 1 − t 2
The area of △ A O B is given by A = 2 a b = t ( 1 − t ) 1 + t to find minimum A , we first find the value of t such that d t d A = 0 and d t 2 d 2 A > 0 .
d t d A t 2 + 2 t − 1 t 2 + 2 t + 1 ( t + 1 ) 2 ⟹ t = t 2 ( 1 − t ) 2 t ( 1 − t ) − ( 1 + t ) ( 1 − 2 t ) = t 2 ( 1 − t ) 2 t 2 + 2 t − 1 = 0 = 2 = 2 = 2 − 1 Putting d t d A = 0 Since t > 0
Since d t 2 d 2 A > 0 , when t = 2 − 1 , A is minimum when t = tan 2 θ = 2 − 1 . ⟹ tan θ = 1 − ( 2 − 1 ) 2 2 ( 2 − 1 ) = 1 ⟹ θ = 4 5 ∘ .