Reach for the Summit - P-S1-A4

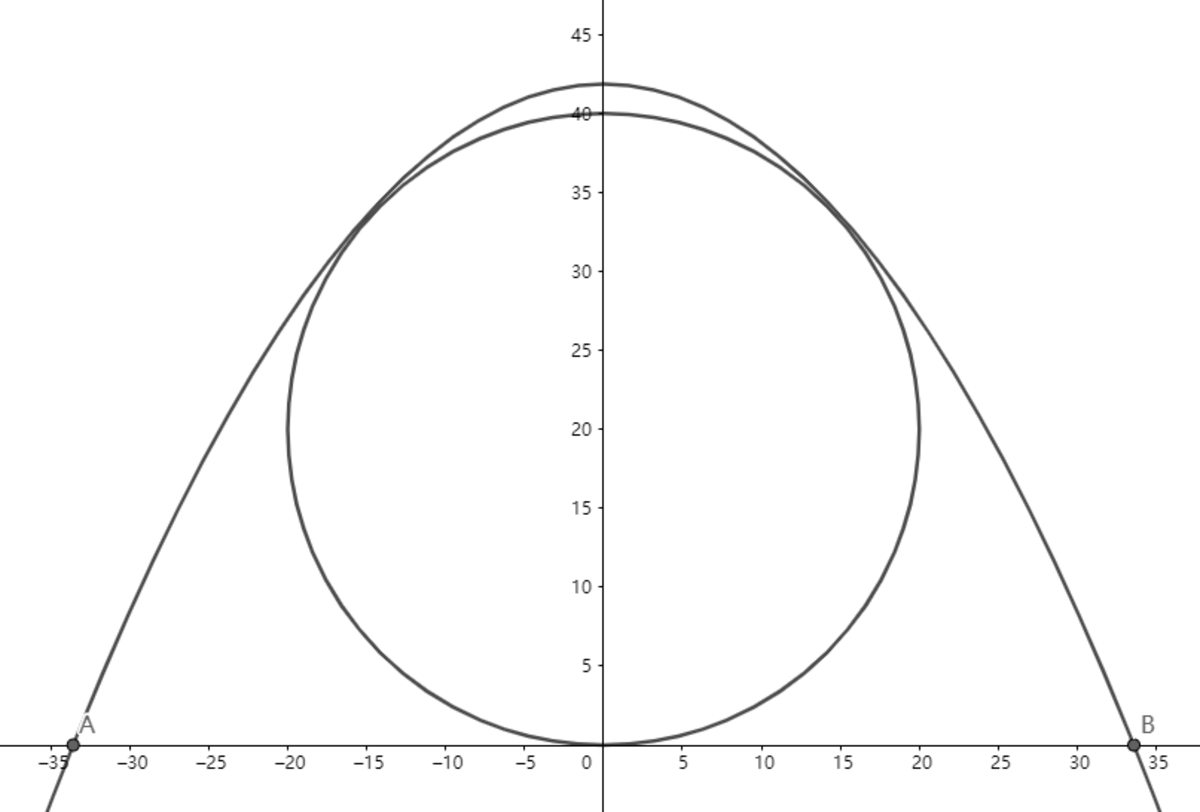
Maximum height attained by a projectile projected at an angle $α$ above horizontal with speed $u$ is

$H=\dfrac {u^2\sin^2 α}{2g}$

Horizontal range of the projectile is

$R==\dfrac {u^2\sin 2α}{g}$ .

Equation of path of the projectile is

$x^2=\dfrac {R^2}{4H}(H-y)$

Equation of the circle is

$x^2+y^2-\dfrac {y}{5}=0$

So the point of intersection of these two curves is obtained from

$y^2-\left (\dfrac {1}{5}+\dfrac {R^2}{4H}\right )y+\dfrac {R^2}{4}=0$

Since the two curves touch each other at this point, we have to have

$\left (\dfrac {1}{5}+\dfrac {R^2}{4H}\right )^2=4\times 1\times \dfrac {R^2}{4}$

$\implies \dfrac {2u^2\cos^2 α}{g}-\dfrac {2u^2\sin α\cos α}{g}+\dfrac {1}{5}=0$

$\implies u^2=\dfrac {1}{\cos α(\sin α-\cos α)}$

This will attain a maximum at $α=\dfrac {3π}{8}$

At this value of angle, the value of $u$ is $2.197368...$ , and the answer is $\boxed {2197}$ .