Read carefully!

Electricity and Magnetism Level 3

A 16 Ω 16 \Omega resistance wire is bent in the form of a square. A source of emf 9 V 9V is connected across one of its sides. If the wire is stretched uniformly to double the length and once again the same cell is connected in same way, across one side of the square formed, what will now be the potential difference across one of its diagonals?


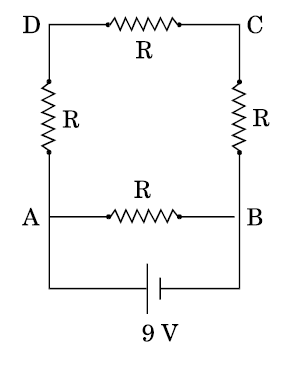
The answer is 6.

Sahil Bansal by Sahil Bansal , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Since the wire has a uniform cross-sectional area, its resistance is proportional to length. Therefore, the 3 3 sides, A D AD , D C DC and C B CB equally divide 9 9 V, with each side 3 3 V, hence the diagonal which has two sides has a potential difference of 6 \boxed{6} V,

5 Helpful 0 Interesting 0 Brilliant 0 Confused

easy soln. I choosed a lengthy method..

Sargam yadav - 4 years, 10 months ago
Sargam Yadav
Jul 21, 2016

Since,the wire is uniform, all the four sides will have equal resistance. When the length of wire is doubled,its area becomes half. So new resistance of wire = 4×16 ohm. Therefore, resistance of each side of square becomes 16ohm. The net resistance of circuit is 12 ohm. Total current passing through circuit is 0.75ohm. So,current passing through all three resistances in series = 0.75/4. Therefore potential difference b/w D and B = 2×(0.75/4)×16=6 V.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...