Ready... And... Slice!
You would like to bisect a triangle, or cut it into two parts of equal area, with a single straight line segment. Here are 3 ways to do it.
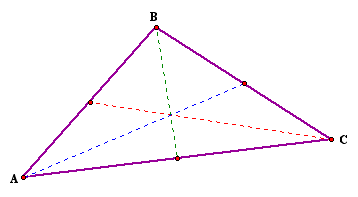
Will all of the infinite possible bisectors pass through the same point?
That is, does there exist a point that all possible bisectors pass through?
Image credit: http://jwilson.coe.uga.edu
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In the figure above, you can see that if such a point exists it would clearly need to be the centroid of the triangle. However any bisecting line drawn parallel to one of the sides will definitely not pass through the centroid of the triangle.
For example, consider the following triangle.
You will see that the horizontal line passing through the centroid splits the triangle into two sections but they are not equal, as the areas have a 5:4 ratio.