Real fun with cyclic quadrilateral
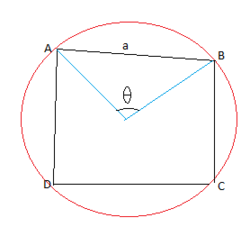 Let a cyclic quadrilateral
inscribed in a circle with a given side length
and
subtends
degree angle at the center of that circle.
Let a cyclic quadrilateral
inscribed in a circle with a given side length
and
subtends
degree angle at the center of that circle.
Maximize the area, of quadrilateral .
If it can be expressed as:
for positive integers , evaluate .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let O as center of given circle { r a d i u s = r } , Clearly in triangle O A B using cosine law a 2 = r 2 + r 2 − 2 r . r cos θ r 2 = 2 ( 1 − cos θ ) a 2
N o t e : Since it is Standard result that area of an standard triangle A B C is Δ = 2 1 b c sin A
Let angle's as ∠ B O C = x 1 , ∠ C O D = x 2 , ∠ D O A = x 3
So Area of quadrilateral is :
A = 2 1 × r 2 ( sin θ + sin x 1 + sin x 2 + sin x 3 )
For to maximize area A , we have to maximize sin x 1 + sin x 2 + sin x 3 where it has constrained that x 1 + x 2 + x 3 = 2 π − θ . For this purpose In my opinion Jenson's Inequality is best .
So consider an function f ( x ) = sin x and Applying Jensen's Inequality , maximum will occur when :
sin x 1 + sin x 2 + sin x 3 = 3 sin ( 3 x 1 + x 2 + x 3 ) ≡ 3 sin ( 3 2 π − θ ) . So Maximum area will be :
A m a x = 2 1 × r 2 ( sin θ + 3 sin ( 3 2 π − θ ) ) A m a x = 4 ( 1 − cos θ ) a 2 × ( sin θ + 3 sin ( 3 2 π − θ ) )
P = 4 , q = 3 , r = 3 , p + q + r = 1 0