Real number probability
The amount 4.5 is split into two nonnegative real numbers uniformly at random. Then each number is rounded to its nearest integer. For instance, if 4.5 is split into 2 and 4 . 5 − 2 , then the resulting integers are 1 and 3, respectively. What is the probability that the two integers sum up to 5?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let S ( x ) : = ⌊ x ⌉ + ⌊ 4 . 5 − x ⌉ where ⌊ x ⌉ is the result of rounding x . We're effectively trying to find the probability that a randomly selected value x on the range 0 ≤ x ≤ 4 . 5 has S ( x ) = 5 .
One can easily see that this occurs 9 4 of the time by looking at the graph of S ( x ) on the interval (as shown below); however, another way to do it is by looking at the conditions on which S ( x ) is 5. We want both x and 4 . 5 − x to round up, which means that for each rounded value of 4 . 5 − x , x must be in the upper-half of its permissible range. For example, if we consider the case where S ( x ) = 1 + 4 = 5 , we want 4 . 5 − x to round to 4 , implying 0 ≤ x ≤ 1 , but then x only rounds to 1 if it's in the upper-half of that interval. This occurs four times (once for each value from 0 to 4 ), but because of the last value being cut in half, we remove one of the 5 possible instances where the sum would be 5 . Thus, 9 4 .
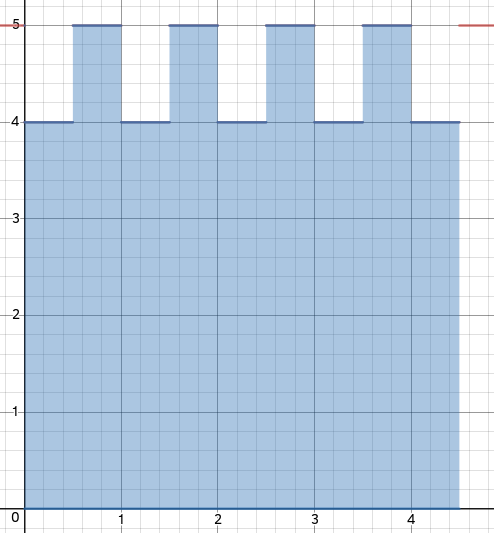
There are 9 possible ranges for the first number, with each having an equal probability:
0-0.5
0.5-1
1-1.5
1.5-2
2-2.5
2.5-3
3-3.5
3.5-4
4-4.5
4 of these ranges will make the sum of the two rounded numbers equal 5:
0.5-1
1.5-2
2.5-3
3.5-4
Therefore, the answer is 9 4