Real roots !!

Algebra Level 2

has which real roots ???

2,17 2,5 10,17 5,10

Shivram Badhe by Shivram Badhe , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

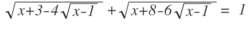
This probably isn't the best solution but I solved it this way.First put 2 in the equation and evaluate to see if the result is 1.It isn't.As both roots are supposed to satisfy the equation,so 1st and 4th option are incorrect(because 2 is not a solution).Try the next option which is 5,10.Evaluate the expression by substituting x x with both of these values and you will get that the R.H.S is equal to 1 so answer is 5 , 10 5,10 .I think verifying the options is easier than solving in this case

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Ultimately even I came down to trial and error, but a little simplification before that came handy.

x + 3 − 4 x − 1 + x + 8 − 6 x − 1 = 1 \sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8-6\sqrt{x-1}}=1

( x − 1 ) − 2 ( x − 1 ) ( 2 ) + 4 + ( x − 1 ) − 2 ( x − 1 ) ( 3 ) + 9 = 1 \sqrt{(x-1)-2\left(\sqrt{x-1}\right)(2)+4}+\sqrt{(x-1)-2\left(\sqrt{x-1}\right)(3)+9}=1

( x − 1 ) 2 − 2 ( x − 1 ) ( 2 ) + ( 2 ) 2 + ( x − 1 ) 2 − 2 ( x − 1 ) ( 3 ) + ( 3 ) 2 = 1 \sqrt{\left(\sqrt{x-1}\right)^{2}-2\left(\sqrt{x-1}\right)(2)+(2)^{2}}+\sqrt{\left(\sqrt{x-1}\right)^{2}-2\left(\sqrt{x-1}\right)(3)+(3)^{2}}=1

( x − 1 − 2 ) 2 + ( x − 1 − 3 ) 2 = 1 \sqrt{\left(\sqrt{x-1}-2\right)^{2}}+\sqrt{\left(\sqrt{x-1}-3\right)^{2}}=1

∣ x − 1 − 2 ∣ + ∣ x − 1 − 3 ∣ = 1 \lvert\sqrt{x-1}-2\rvert+\lvert\sqrt{x-1}-3\rvert=1

This makes trial and error easier.

Omkar Kulkarni - 6 years, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...