Real world Birthday Paradox

Probability Level 3

Birthday problem : What is the smallest value of $n$ such that out of $n$ randomly selected people, the probability that at least two of them share the same birthday exceeds 50%?

Making the assumption that birthdays are equally distributed, we conclude that the answer is 23. In reality, birthdays are unevenly distributed, and are more frequent in the summer months of July, August, September and October.

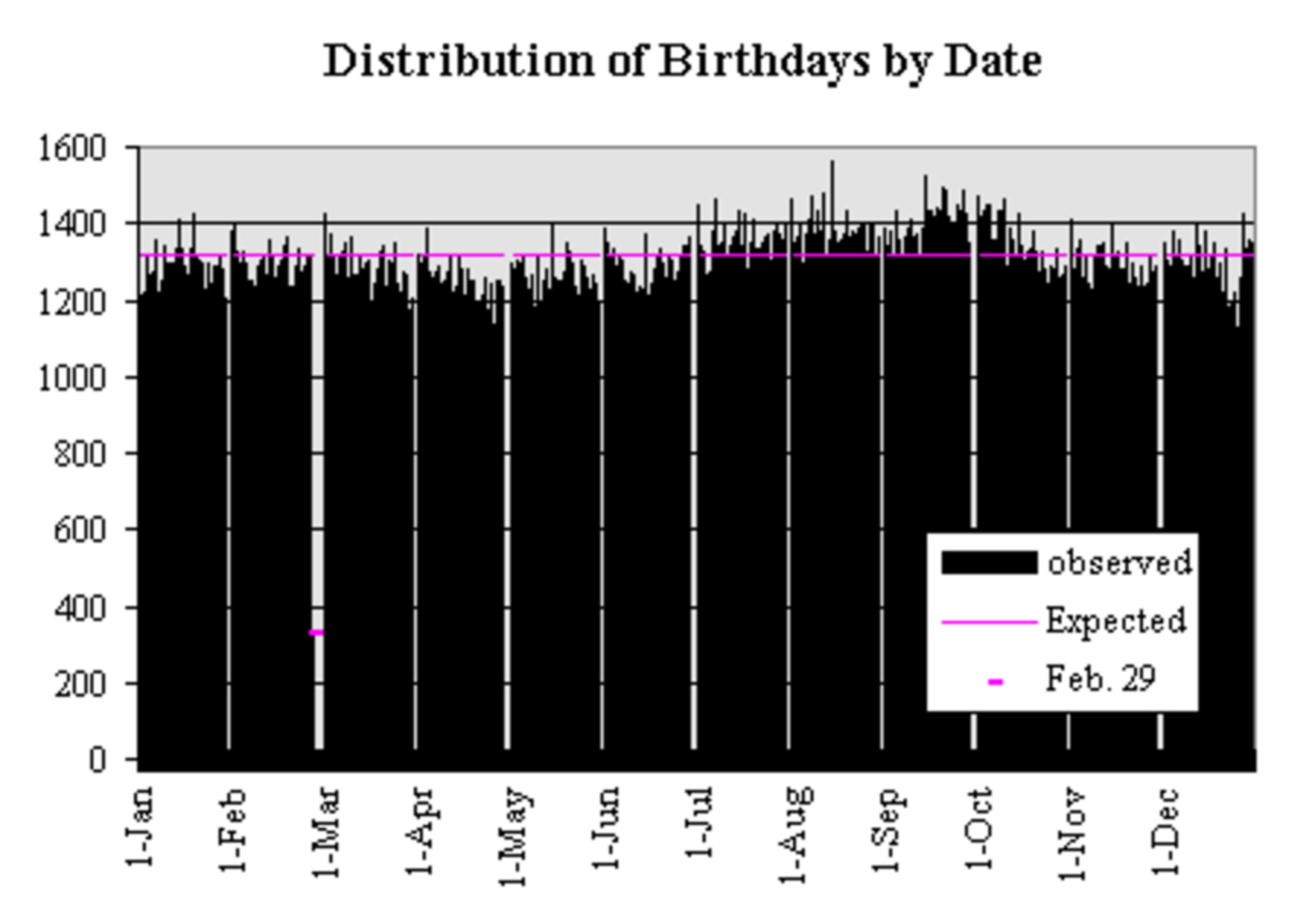Distribution of birthday by date, sample population in United States

Given that the distribution isn't uniform, how would this impact the final analysis?

Reduce the number of people needed Increase the number of people needed No change to the number of people needed Direction of change is unkown

1 solution

Brian Charlesworth
Jan 9, 2017

The more calender-concentrated the birthdays are, the more likely two of the randomly chosen people will have the same birthday. Taking a somewhat extreme case for purposes of demonstration, suppose $all$ people in general are born in the four months listed. Assuming an even distribution within this 123-day time period, we would be looking for the minimum value of $n$ such that

$1 - \dfrac{123*122*121*....*(123 - (n - 1))}{123^{n}} \ge 0.5$ ,

which turns out to be $n = 14$ . Any peaks in the distribution, even if they aren't concentrated in one continuous period but occur in more than one peak, will have the same effect.

@Chung Kevin The boxed paragraph looks good now. In the next paragraph it might be an idea to go with "Making the assumption that each birthday is equally likely, ....". Fun problem; it made me think a bit until I came up with the "extreme case" approach. There appears to be a notably wide dip in the graph just before Christmas: I wonder what's the cause of that anomaly?

Brian Charlesworth - 4 years, 5 months ago

Thanks for catching these errors. I was moving parts of the problem around, and should have proof-read it again.

Your explanation still allows for "direction of change is unknown". We have to show that any deviation from the uniform distribution would lead to a lower value (ignoring the rounding effect). This has to do with inequalities, with the equality case occurring when the distribution is uniform.

The increase in July-Oct is often explained by the lack of activities during winter. I guess when spring rolls around, people are eager to head outside instead of staying indoors.

Chung Kevin - 4 years, 5 months ago

Real world Birthday Paradox

1 solution

0 pending reports