Really E-Z
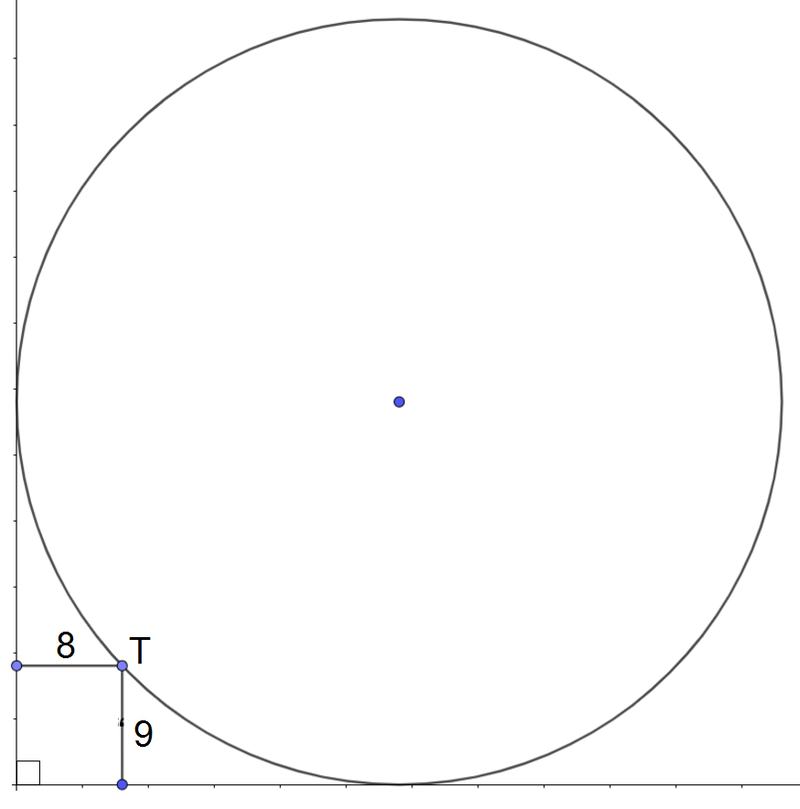
A circle touches two perpendicular lines with point T being 8 and 9 units form the two lines as shown in the figure. Find the radius of the circle.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Why do you all exclude the case when radius is 5. It is valid as well as the radius 29. But the circle will be "inside" the rectangle 8,9.
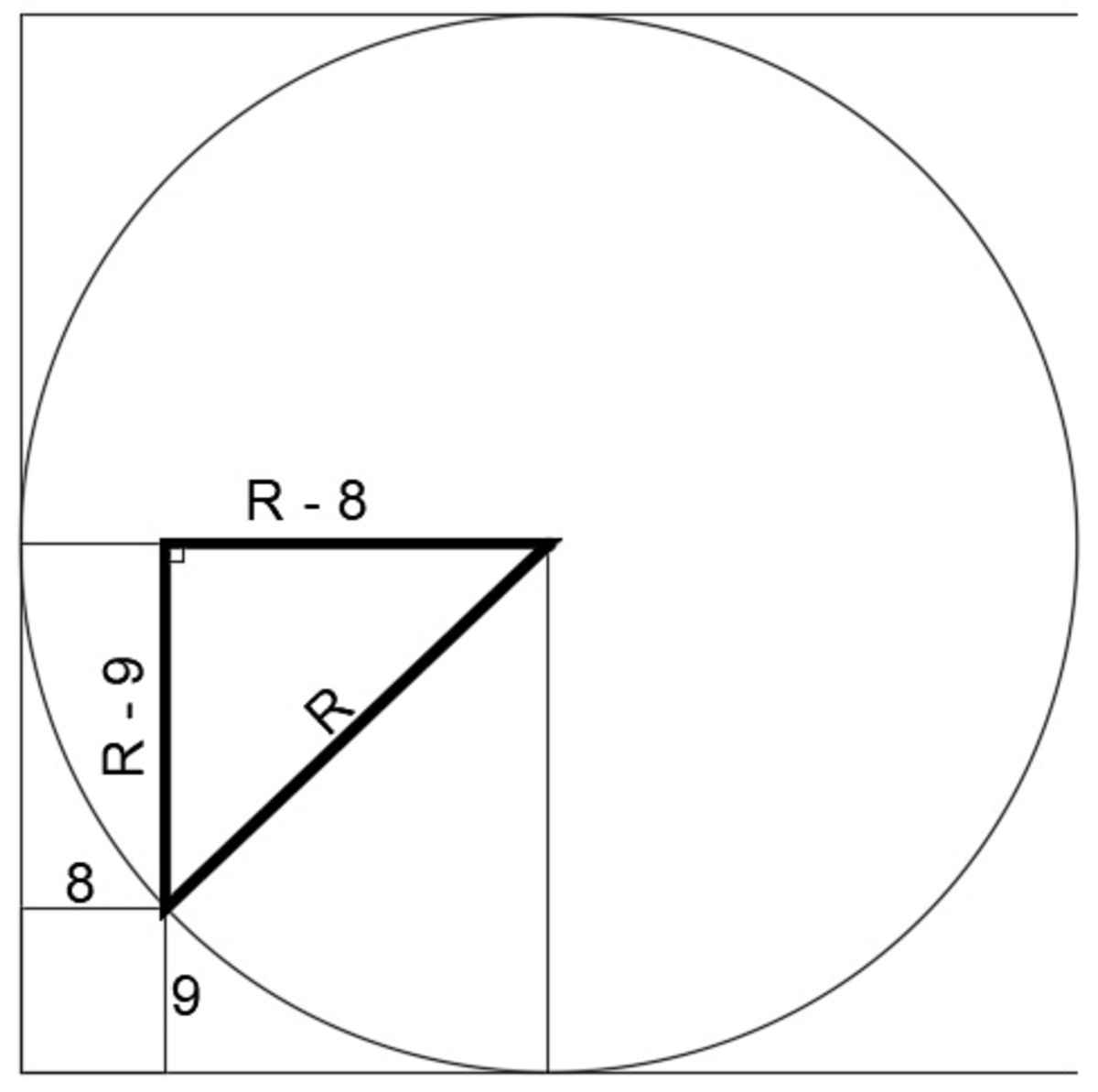
R 2 = ( R − 8 ) 2 + ( R − 9 ) 2
R 2 = ( R 2 − 1 6 R + 6 4 ) + ( R 2 − 1 8 R + 8 1 )
R 2 = R 2 − 1 6 R + 6 4 + R 2 − 1 8 R + 8 1
0 = R 2 − 3 4 R + 1 4 5
R = 2 a − b ± b 2 − 4 a c = 2 ( 1 ) − ( − 3 4 ) ± ( − 3 4 ) 2 − 4 ( 1 ) ( 1 4 5 ) = 2 3 4 ± 2 4
R = 2 3 4 + 2 4 = 2 9 or R = 2 3 4 − 2 4 = 5
Answer: R = 29 units
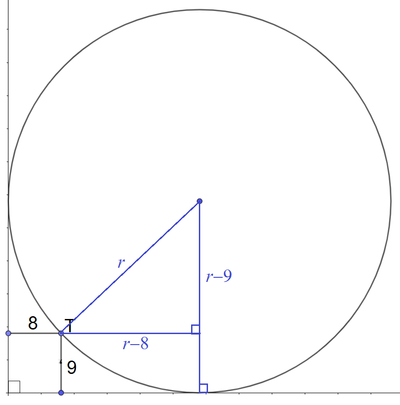
Let the radius of the circle be r . We can see from the figure that by Pythagorean theorem :
( r − 8 ) 2 + ( r − 9 ) 2 r 2 − 1 6 r + 6 4 + r 2 − 1 8 r + 8 1 r 2 − 3 4 r + 1 4 5 ( r − 5 ) ( r − 2 9 ) ⟹ r = r 2 = r 2 = 0 = 0 = 2 9 Since r > 5
@Ricky Huang , you should not have included the figure with numbers on the x - and y -axes, because member can just guess the radius from the numbers. I have redone the figure for you.
Let the radius of the circle be r . Then
( 8 − r ) 2 + ( 9 − r ) 2 = r 2 ⟹ r 2 − 3 4 r + 1 4 5 = 0 ⟹ r = 2 9 (since r > 9 ).
Although this is not much of an explanation, I graphed as follows and got the radius to be 2 9 .