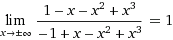The unnecessary value
x 3 − x 2 + x − 1 x 3 − x 2 − x + 1 = 0 , x = ?
The answer is -1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Factor the numerator and denominator by grouping and simplify. Then find the value of x that would make the numerator equal to 0.
You should mention that even though 0 = x 3 − x 2 − x + 1 = ( x − 1 ) 2 ( x + 1 ) has a solution x = 1 , that is not the solution to the equation because x = 1 would make the denominator 0, and hence the expression would be undefined.
Log in to reply
I put it that way purposely because I want it to be more than just solving the equation.
Log in to reply
I meant "mention in your solution". This allows others who were unable to solve the problem, to then learn from your solution.
Your solution is currently too abbreviated. Those who have solved the problem can understand what you are thinking. Those who have not solved the problem, are unable to read your mind to understand how to approach the solution.