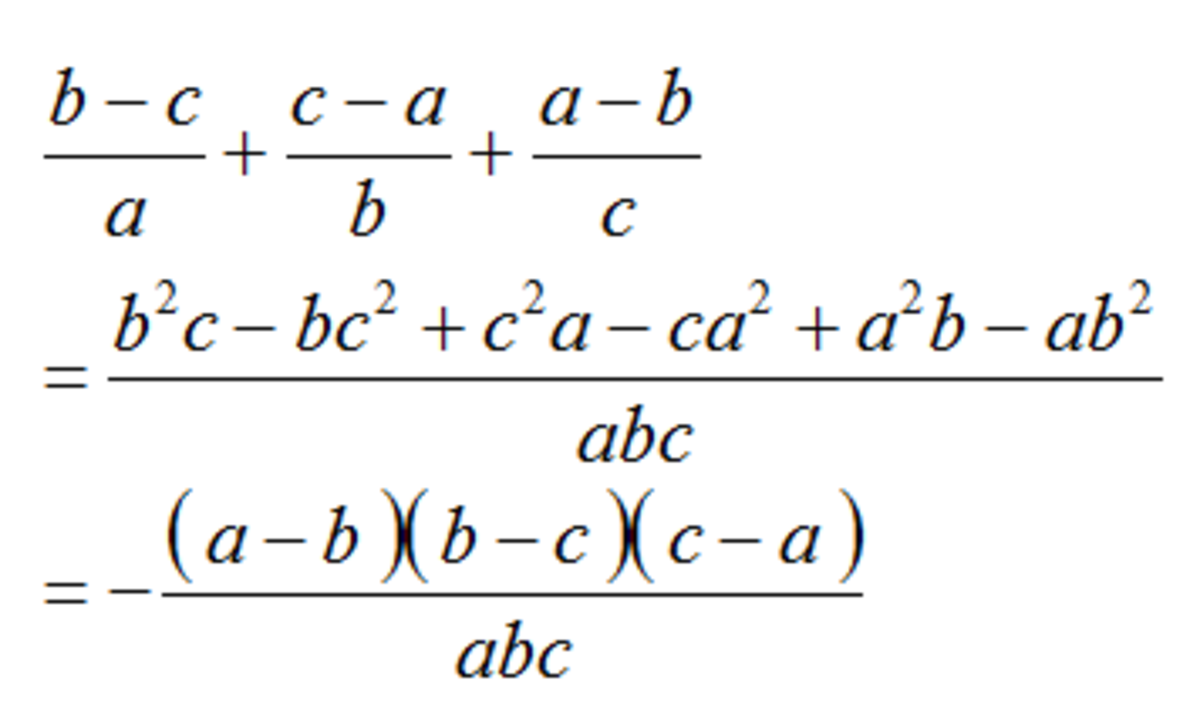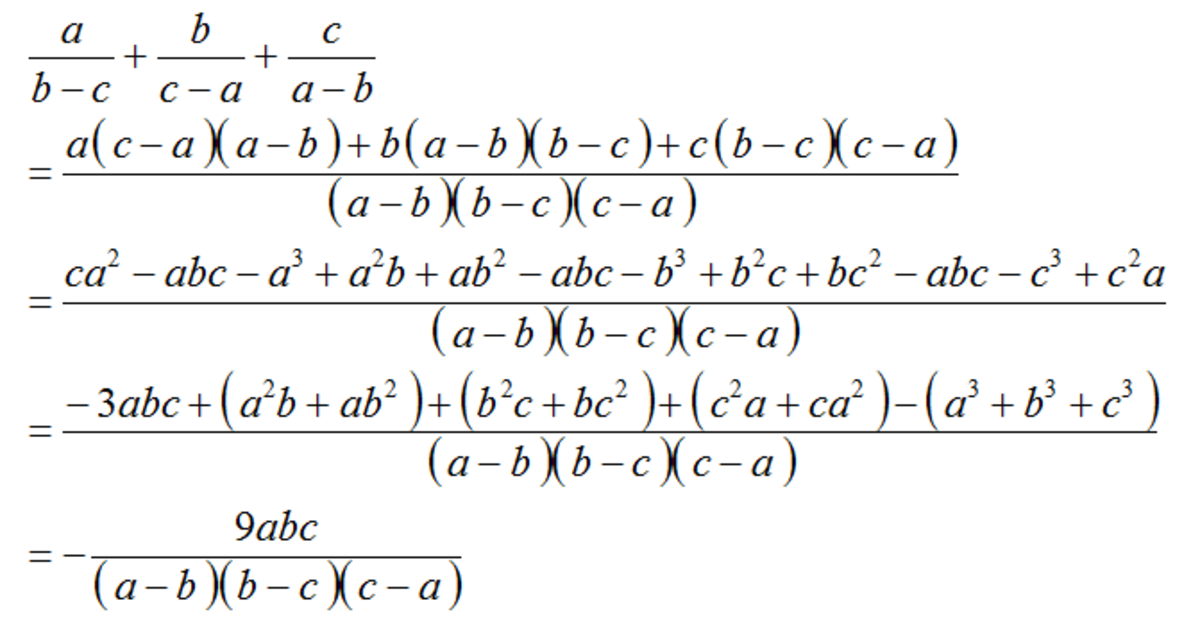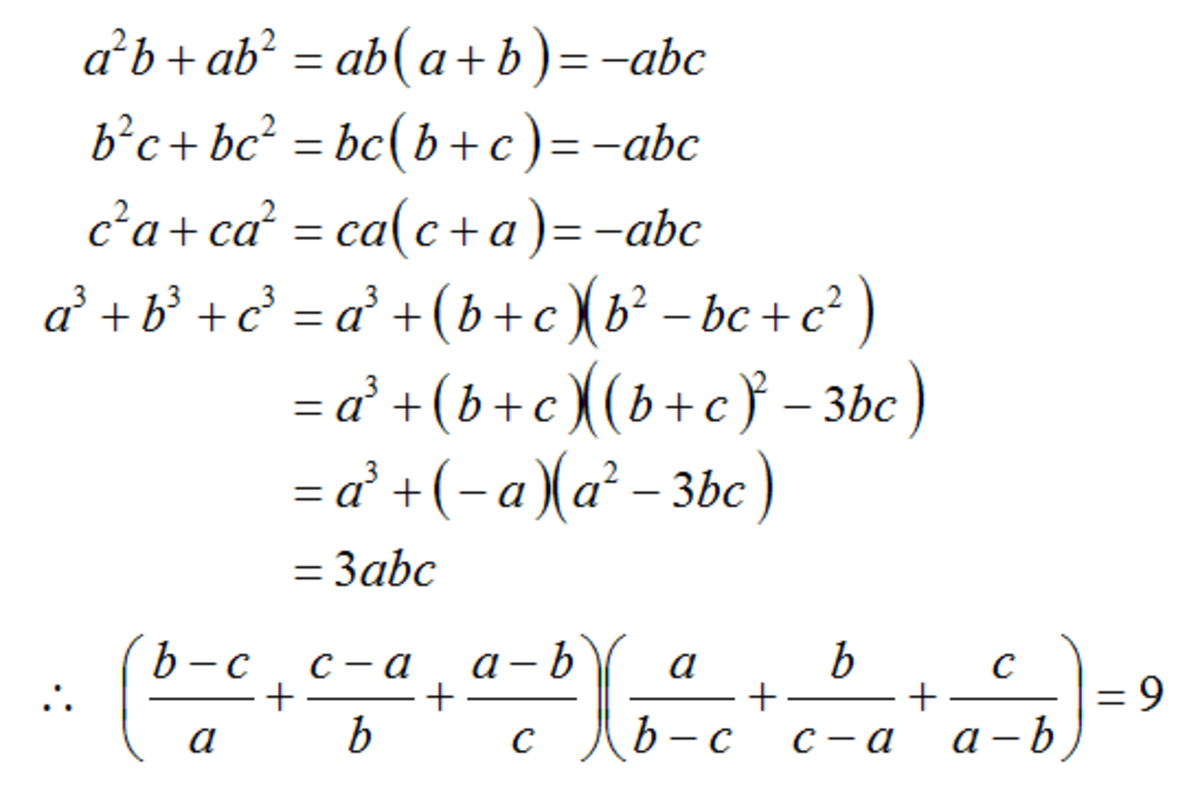Really tough

Algebra Level 4

( b − c a + c − a b + a − b c ) ( a b − c + b c − a + c a − b ) \large{\left(\dfrac {b-c}{a}+\dfrac {c-a}{b}+\dfrac {a-b}{c}\right)\left(\dfrac {a}{b-c}+\dfrac {b}{c-a}+\dfrac {c}{a-b}\right)}

If a + b + c = 0 a+b+c=0 , then find the value of the expression above.


The answer is 9.

View wiki
Atul Shivam by Atul Shivam , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

汶良 林
Oct 19, 2015

4 Helpful 0 Interesting 0 Brilliant 0 Confused
Nivedit Jain
Jun 2, 2017

Better way to do it take a,b and c as cube roots of unity.

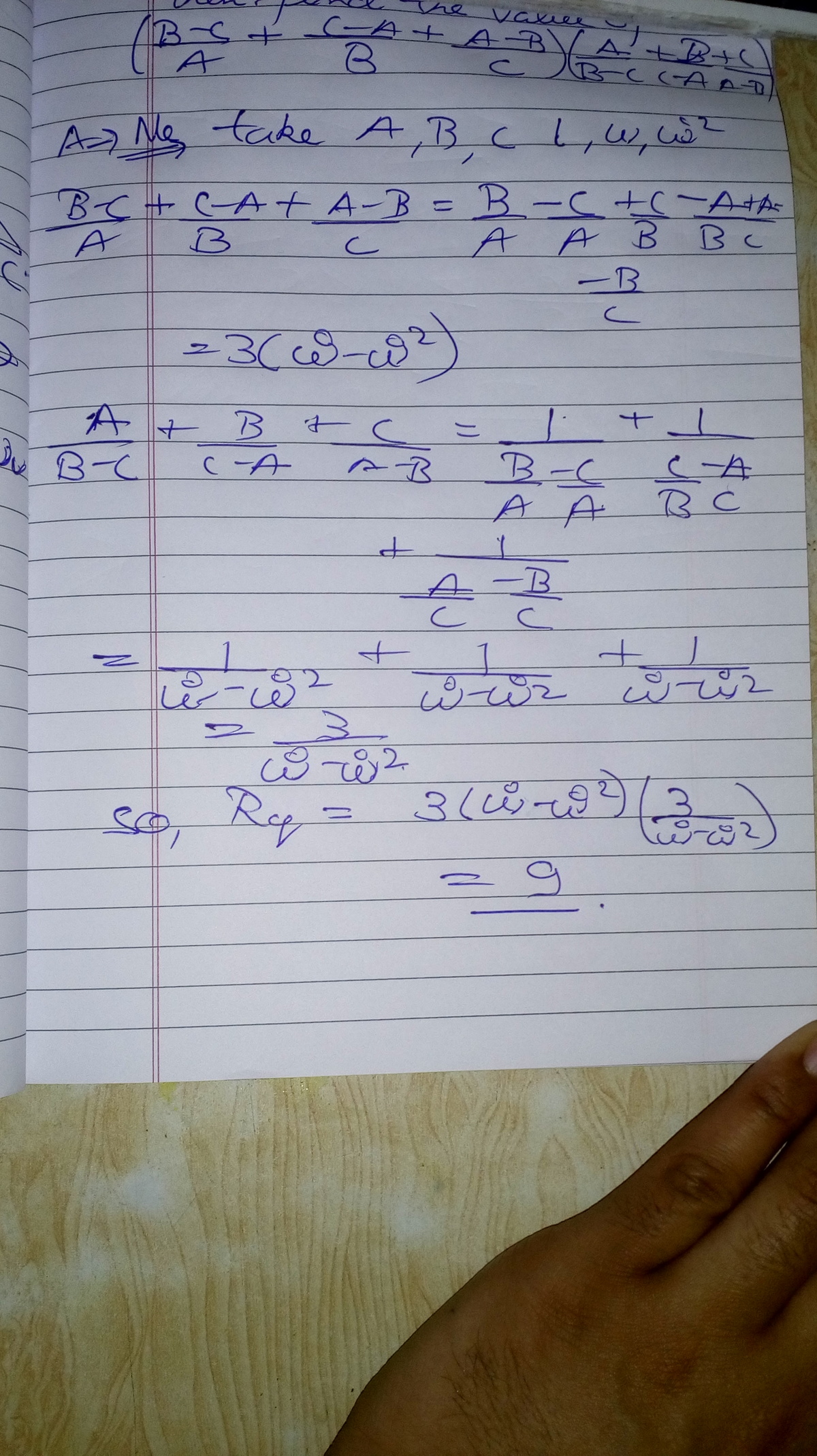
2 Helpful 0 Interesting 0 Brilliant 0 Confused

Innovative approach. Since the problem doesn't state anything about the numbers a,b,c one could assume them to be anything.

Nishant Sharma - 2 years, 12 months ago
Rhealyn Alba
Oct 18, 2015

Assign values of a, b and c that could give an answer 0 when added. As for me, I've used a= 3, b= 2, c= -5. Then substituted them all to the expression. It gives an answer of 9. :)

0 Helpful 0 Interesting 0 Brilliant 0 Confused

I think you should generalise it for all values,without taking any specific value,thanks

Atul Shivam - 5 years, 7 months ago

One can assign any value for a, b, c, if it satisfies a+b+c=0 and none equal to 0 or to one another.( Divide by 0 not valid.)
That will give the answer. But not good as proof.

Niranjan Khanderia - 2 years, 7 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...