Recalling sir Euler

Sir Euler once said

$e^{i \phi} = \cos(\phi)+ i \sin(\phi)$

so $e^{i \pi} = \cos(\pi)+i\sin(\pi) = -1+0=\boxed{-1}$

For anyone who hasn't seen this done out:

Apply the Maclauran series for e^(x)

$e^{i\pi} = 1 + i\pi + \frac{(i\pi)^{2}}{2} + \frac{(i\pi)^{3}}{3!} + \frac{(i\pi)^{4}}{4!} + \frac{(i\pi)^{5}}{5!} + \frac{(i\pi)^{6}}{6!} + \frac{(i\pi)^{7}}{7!} + \frac{(i\pi)^{8}}{8!}$ ...

simplify the i's

$= 1 + i\pi - \frac{\pi^{2}}{2} - i\frac{\pi^{3}}{3!} + \frac{(\pi)^{4}}{4!} + i\frac{(\pi)^{5}}{5!} - \frac{(\pi)^{6}}{6!} - i\frac{(\pi)^{7}}{7!} + \frac{(\pi)^{8}}{8!}$ ...

distribute

$= (1 - \frac{\pi^{2}}{2} + \frac{(\pi)^{4}}{4!} - \frac{(\pi)^{6}}{6!} + \frac{(\pi)^{8}}{8!}...) + i (\pi - \frac{\pi^{3}}{3!} + \frac{(\pi)^{5}}{5!} - \frac{(\pi)^{7}}{7!}...)$

Apply the Maclauran series for sin(x) and cos(x)

$= cos(\pi) + i \times sin(\pi)$

simplify

$= -1 + i \times 0 = -1$

Therefore:

$e^{i\pi} = -1$

If you visualise it using imaginary numbers in exponential form on an argand diagram it makes it a lot easier

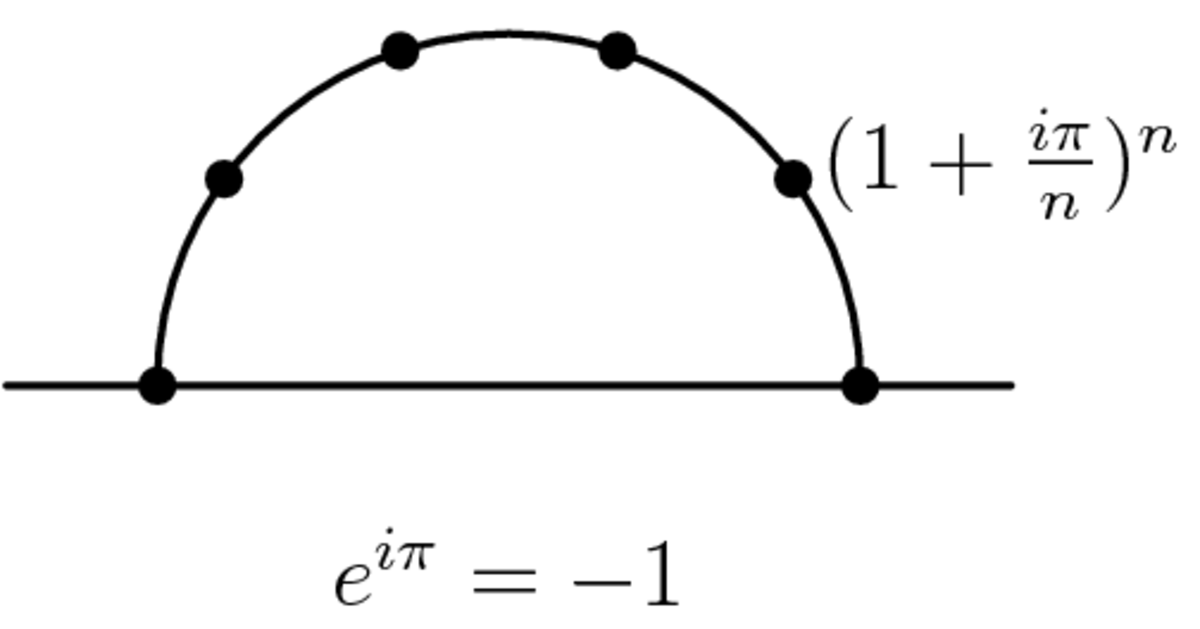
Another "solution" (not very rigorous). We know that $e$ is the limit as x goes to infinity of $\left(1 + \frac{1}{x}\right)^x$ , and that $e^z$ is the limit of $\left(1 + \frac{z}{x}\right)^x$ . Now, let us look at the complex plane. If we draw the top half of the unit circle, and then divide it into $n$ parts, we notice a few things. First, we see that the rightmost point no on the x-axis to the $n$ is -1. Next, we also see that as $n$ becomes arbitrarily large, that same rightmost point goes to $1+\frac{i\pi}{n}$ . Finally, piecing this together we have $(1+\frac{i\pi}{n})^n = -1$ which, by the first part is the same as $e^{i\pi} = -1$ .

Let z = cos(x) + i.sin(x)

   dz/dx = -sin(x) + i.cos(x)

         = i[cos(x) + i.sin(x)]

   dz/dx = i.z

 so dz/z = i.dx

INT[dz/z] = INT[i.dx]

   ln(z) = i.x + const

       z = e^(i.x + const)

Now from z = cos(x) + i.sin(x) when x=0, z=1 so the constant = 0

Thus z = e^(i.x)

That is cos(x) + i.sin(x) = e^(i.x)

When x = pi -1 = e^(i.pi)

Euler formula.....

e^(i*pi) = -1 + 0 i = -1 ; I worked it in GeoGebra. A soft-ware free down-load from GeoGebra.org

Euler's Identity is as follows:

$e^{i\pi}+1=0$

We can subtract $1$ from both sides to give us $e^{i\pi}=-1$

Cause Euler said so

Simple, just use Euler's formula

Let z = cos(x) + i.sin(x) dz/dx = -sin(x) + i.cos(x) = i[cos(x) + i.sin(x)] dz/dx = i.z so dz/z = i.dx INT[dz/z] = INT[i.dx] ln(z) = i.x + const z = e^(i.x + const) Now from z = cos(x) + i.sin(x) when x=0, z=1 so the constant = 0 Thus z = e^(i.x) That is cos(x) + i.sin(x) = e^(i.x) When x = pi -1 = e^(i.pi) 0 = e^(i.pi) + 1 or e^(i.pi) + 1 = 0

EULER Theorem bro!!!! let @ be theta (just consider).....

     i[@]
  e                 =      cos@ + i sin@

so e ^i(180 ) = cos 180 + i sin 180* = -1 + 0 i =-1 :)

its a different form of representation of a complex number...it stands for - ( cos(pie) + iota*sin(pie)

In response to Michael Fuller I think sin (eln(pi)) is equal to 0.02988975.

e^(iQ)= cos(Q) + isin(Q)

So, the answer is -1