Recapitulation
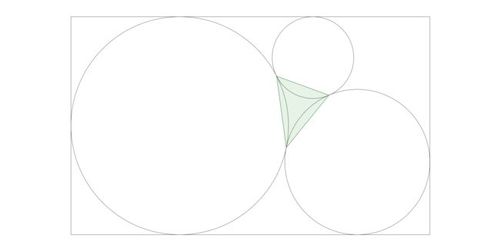 Three circles are enclosed in a rectangle such that each circle is tangent with one another and the rectangle.
The dimensions of the rectangle are
by 24.
A triangle is formed using the points of tangency of the circles as vertices.
Three circles are enclosed in a rectangle such that each circle is tangent with one another and the rectangle.
The dimensions of the rectangle are
by 24.
A triangle is formed using the points of tangency of the circles as vertices.
Find the area of the triangle, which can be expressed as the expression in lowest terms, where , and are integers. Submit your answer as .
The answer is 13477.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The radii of the circles can be obtained: r 1 = 2 4 / 2 = 1 2 , r 2 = 8 , r 3 = 4 . 5 The triangle in question is in fact contact triangle for the reference triangle having circle centres as its vertices. Using formula for the contact triangle area where s denotes reference triangle semiperimeter and △ its area:
a b c ∗ s 2 △ 3 = 1 3 7 5 1 2 0 9 6 6