Recollect the past 3!
Determine the horizontal velocity with which a stone must be projected horizontally from a point , so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is and point is at a height above the foot of the incline.
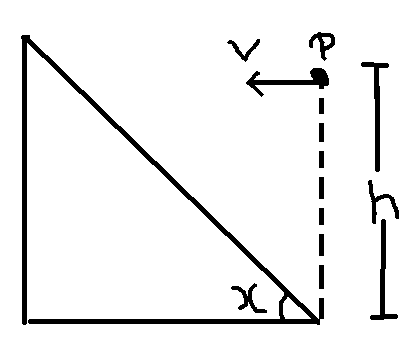
Details And assumptions
Take
Round off the answer to the nearest integer.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For the stone to hit the inclined plane perpendicularly, it must make an angle of 4 5 ∘ below the horizontal, therefore, the instantaneous vertical velocity u is the same as v . Therefore, v = u = g t , where t is the time lapse after the stone is projected. Now, the horizontal and vertical displacements x and y respectively of the stone are as follows:
{ x = v t y = 2 1 g t 2 = 2 1 v t = 2 x ⇒ x = 2 y
Since the plane is inclined at 4 5 ∘ , is horizontal distance is y lesser for every y vertical drop of the stone. Therefore, the stone hits the inclined plane after falling y = 3 1 0 m (see diagram below).
From y = 2 1 g t 2 ⇒ t = 3 2 and v = g t = 1 0 3 2 = 8 . 1 6 4 9 ≈ 8 .