Recollect the past 7!

A Particle is projected from $O$ on the ground with velocity $u$ at an angle $x$ with the horizontal. It strikes at a point $C$ on a fixed smooth plane $AB$ having inclination theta with the horizontal as shown in the figure below. If the particle does not rebound from the plane, then find maximum height from the ground to which the particle rises.

Details And Assumptions :

The particle does not get stuck to the plane at point of striking(Point C in the figure) that is it can move further on the plane. The collision is perfectly inelastic and particle can move along the plane

All the given Below details are in SI Units

$\tan(x) = 0.5$ , $\sin(\theta) = 0.6$ , $g = 10$ , $u = 5\sqrt5$ .

OA = 10/3 m

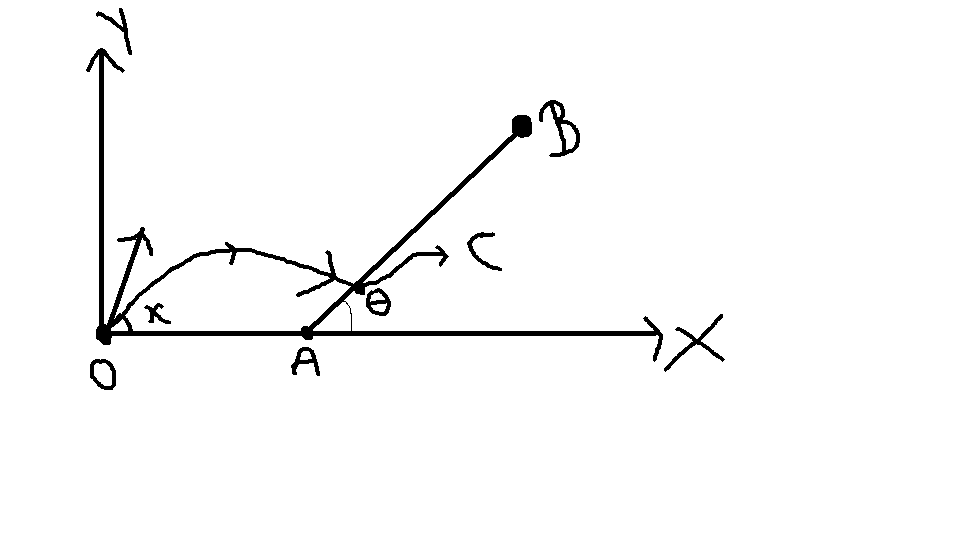
For the problem writing party.