Rectangle Inception
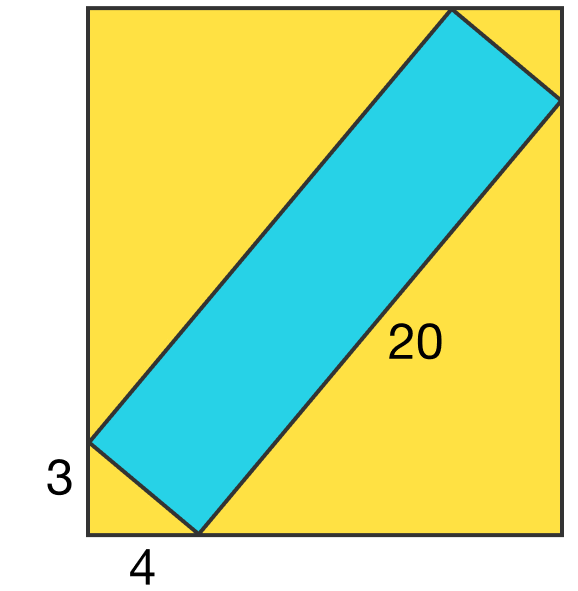
A blue rectangle is placed within a yellow rectangle, and some of the lengths are shown.
What are the dimensions of the yellow rectangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Can you clarify why the four triangles are congruence? I couldn't prove it.
Log in to reply
They aren't congruent, they are similar! Suppose the upper-left vertex of the yellow rectangle is A , the upper-right B , and so on until D . Now, suppose the vertex of the blue rectangle that is above D is E , the one to the left of B is F and so on until H ; In △ E D H , the upper angle is α , and the lower angle (not the right angle) is β . So, α + β = 9 0 ° . We also have ∠ D H E + ∠ E H G + ∠ G H C = 1 8 0 ° ⟼ β + 9 0 ° + γ = 1 8 0 ° ⟼ β + γ = 9 0 ° ⟼ γ = α . Finally, we can conclude that △ E D H is similar to △ H C G . The same process aplies for the others.
I did the same way. Similar triangle have their sides in same ratio.
If hypotenuse is 20, then possible sides are 16,12 or 12,16. So answer would be 20 X 15 or 16 X 19. The second matches with given options.
I don't think that conclusion can be drawn. There should be infinitely many pairs of sides where the hypotenuse is 20. Right?
First of all, we have two small right triangles with legs 3 and 4, so the hypotenuse is 3 2 + 4 2 = 9 + 1 6 = 2 5 (it's the most famous pythagorean triple, by the way). Then, we can see that the two big right triangles are similar to the small ones by analyzing the angles. We just need to know how much times bigger it's than the small ones. So, we have: 5 2 0 = 4 . Four times bigger :D Now, paying attention to the angles, the down leg is 4 × 3 = 1 2 and the other is 4 × 4 = 1 6 .
Finally, the sides of the rectangle are 4 + 1 2 = 1 6 and 1 6 + 3 = 1 9 . 1 6 × 1 9