Rectangle inscribed in a triangle

There is a nice relation between the sides of the rectangle inscribed and the base and height of the triangle. It is given below.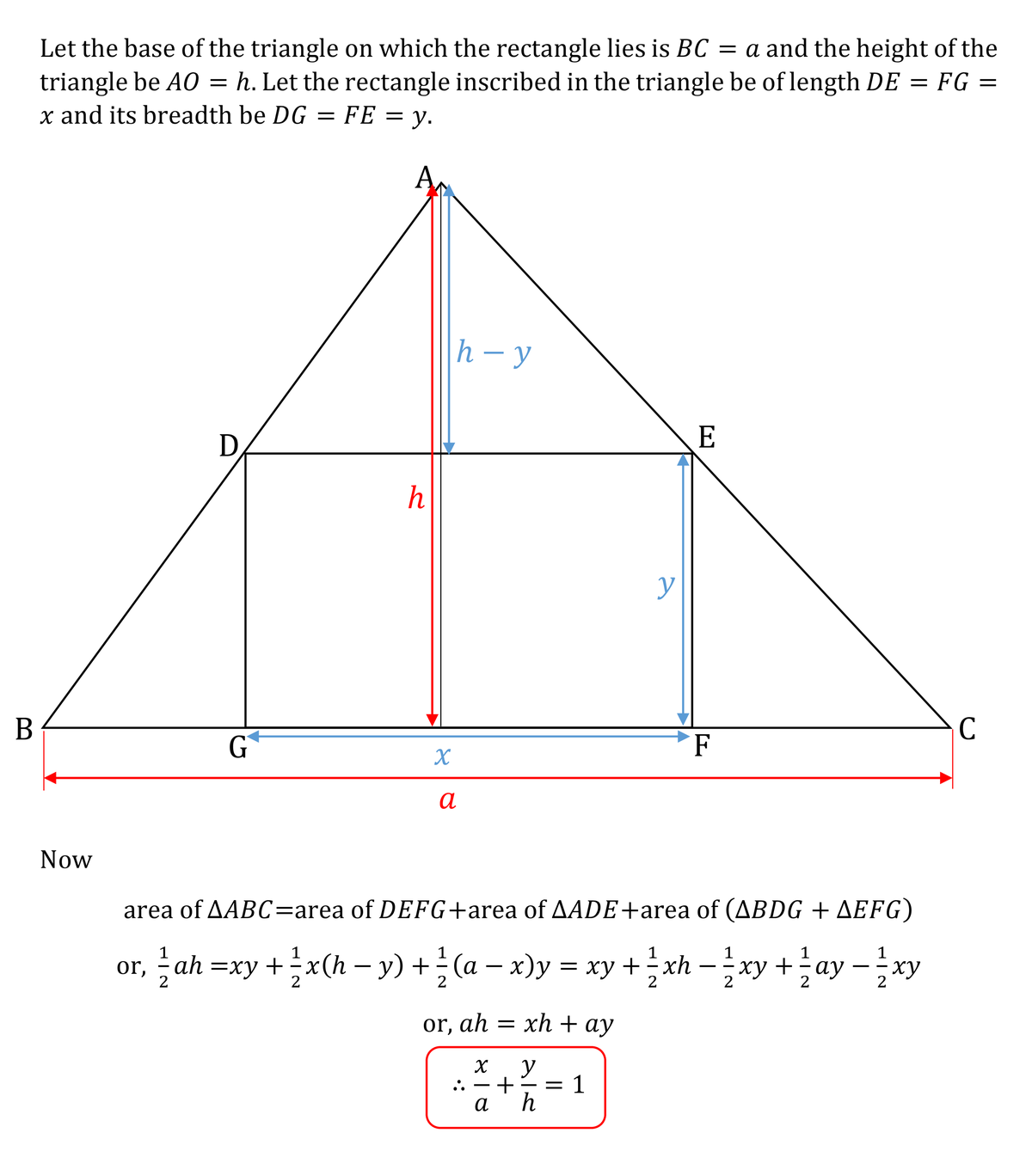 So $\large \frac{x}{a}+\frac{y}{h}=1$ which is analogous to the intercept form of straight line. [Can someone give me an intuition of this?]

According to the question

$\large \frac{\frac{5}{3}}{a}+\frac{3.5}{h}=1$ or $\large \frac{3.5}{a}+\frac{\frac{5}{3}}{h}=1$

Solving, $h=4,a=6$ or $h=6,a=4$

So for this triangle $\large \frac{x}{4}+\frac{y}{6}=1$ or $\large \frac{x}{6}+\frac{y}{4}=1$

or , $2x+3y=12$ or $3x+2y=12$

or, $\large y=\frac{12-3x}{2}$ or $\large y=\frac{12-2x}{3}$

Let $\large A$ be the area of the rectangle. So $\large A=xy=\frac{12x-3x^2}{2}$ or $\large \frac{12x-2x^2}{3}$

or, $\large \frac{dA}{dx}=6-3x$ or $\large \frac{dA}{dx}=4-\frac{4}{3}x$

In both cases the 2nd differential will be negative so $A$ is largest when $\large \frac{dA}{dx}=0$

So, $x=2$ or $x=3$

Putting these values in the respective equations of $A$ we get that in both cases $\large A_{max}=\boxed{6}$