Rectangle inscribed of circle

Let’s call the sides of the rectangles $x$ and $y$ and call the radius $r$ . By our given information, twice the area of the rectangle is equal to the area of the circle. Our equation is: $2xy=\pi r^2$ Now we can use the Pythagorean Theorem for a second equation because we can form a right triangle with the sides of the triangle as legs and the diameter ( $2r$ ) as the hypotenuse: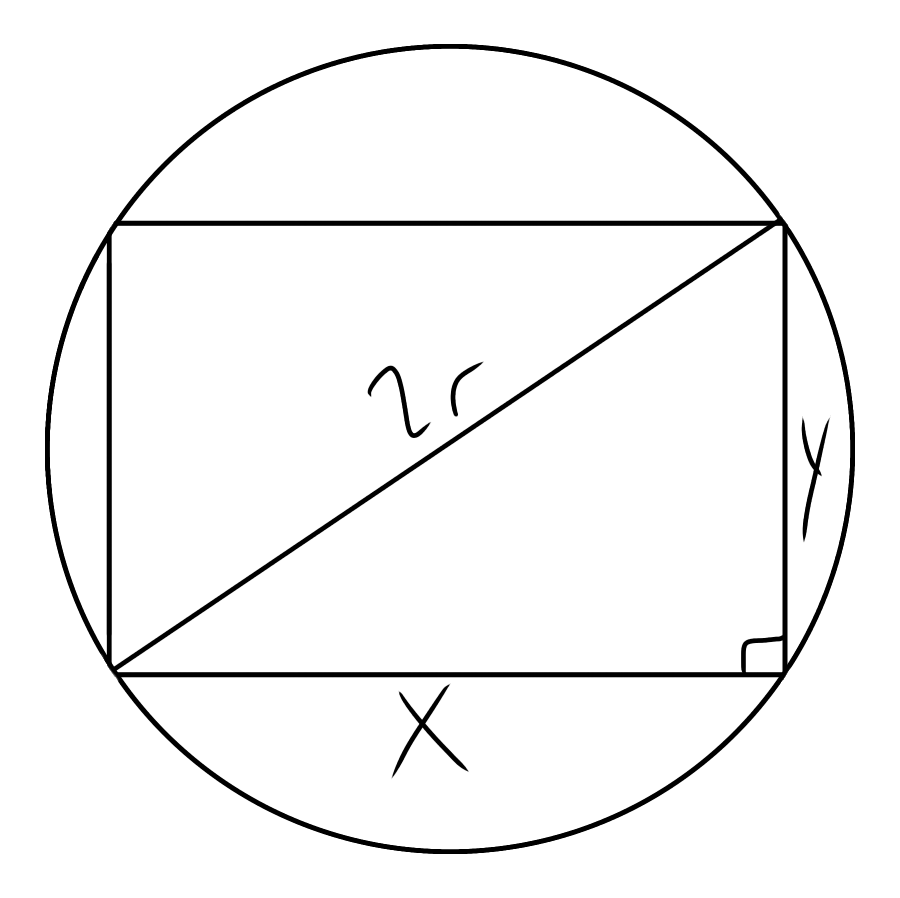 $x^2+y^2=4r^2$ Our goal is to find what $\frac{x}{y}$ is, so we can cancel out the $r^2$ term by dividing our two equations by each other: $\frac{2xy}{x^2+y^2}=\frac{\pi}{4}$ Cross multiply: $8xy=\pi x^2+\pi y^2$ Move everything to one side: $\pi x^2-8xy+\pi y^2=0$ At first, factoring this seems impossible. However, remember that we are looking for $\frac{x}{y}$ . It would make this problem easier if we could turn our quadratic into one variable. In this case, since we are looking for $\frac{x}{y}$ , we would want an equation in the form of $a \left(\frac{x}{y} \right)^2+b \left(\frac{x}{y} \right)+c=0$ . This can be acheived by diving the equation by $y^2$ : $\pi \left(\frac{x}{y} \right)^2-8 \left(\frac{x}{y} \right)+\pi=0$ To find what $\frac{x}{y}$ is, we can use the quadratic formula: $\frac{x}{y}=\frac{8 \pm 2\sqrt{16-\pi^2}}{2\pi}$ Which simplifies to: $\frac{x}{y}=\frac{4 \pm \sqrt{16-\pi^2}}{\pi}$ Now we have two answers. One of these answers is the one when $x$ is the longer side (in which the answer is bigger) and one of them is when $x$ is the shorter side (in which the answer is smaller). We choose the bigger value to find our answer: $\large{\boxed{\frac{4+\sqrt{16-\pi^2}}{\pi}}}$