Rectangle minimum
Rectangle with sides 3 and 4 is given. On each side point is chosen and connected to other two points on adjacent sides. Let S be a sum of lengths of new segments (pink on picture). Find minimum of S.
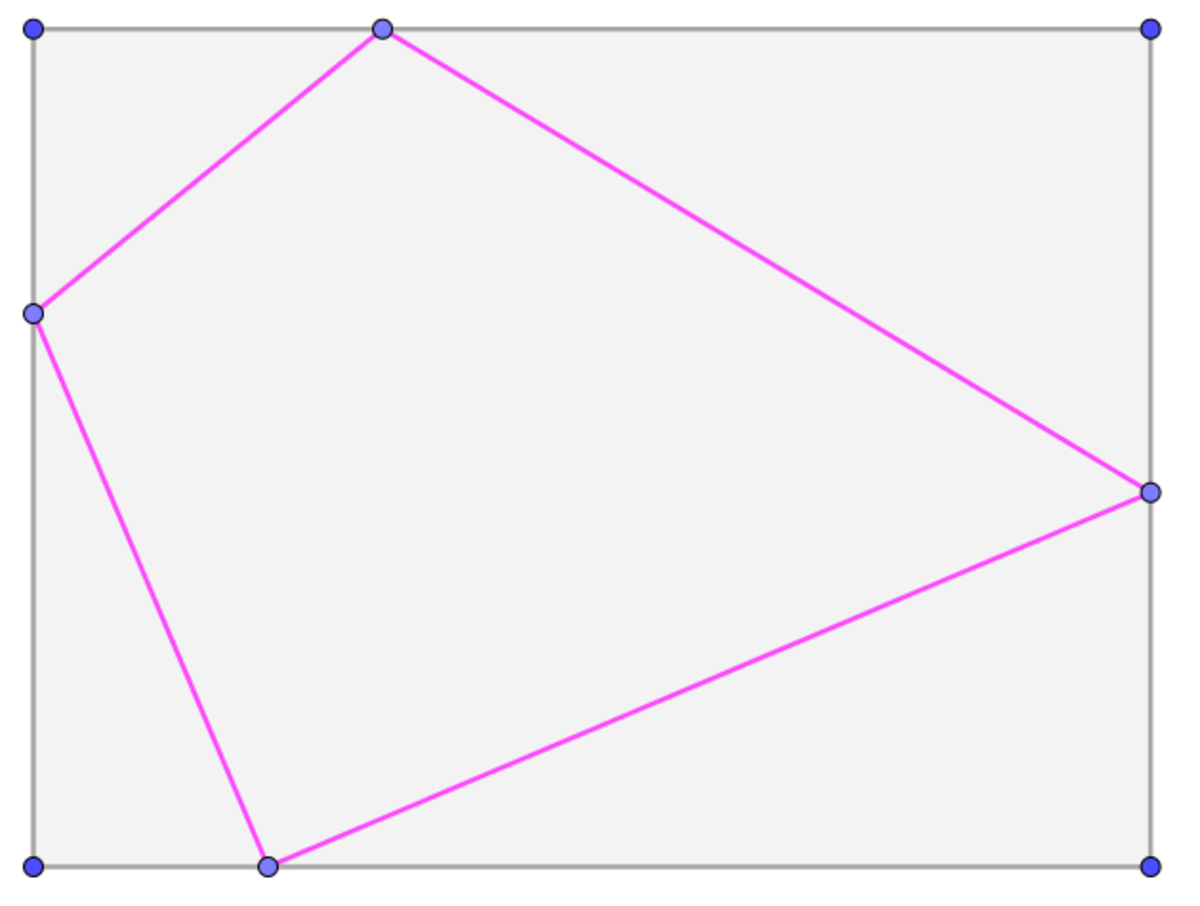
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Usefull inequality: ∑ i = 1 n x i 2 + y i 2 ⩾ ( ∑ i = 1 n x i ) 2 + ( ∑ i = 1 n y i ) 2
Lets mark segments of rectangle with a and b , and smaller segments by a 1 and b 1 , a 2 and b 2 , a 3 and b 3 , a 4 and b 4 , counterclockwise from bottom right vertex. Then, our S is, by Pitagora, b 1 2 + a 2 2 + b 2 2 + a 3 2 + b 3 2 + a 4 2 + b 4 2 + a 1 2 . By usefull inequality: b 1 2 + a 2 2 + a 3 2 + b 2 2 + b 3 2 + a 4 2 + a 1 2 + b 4 2 ⩾ ( b 1 + a 3 + b 3 + a 1 ) 2 + ( a 2 + b 2 + a 4 + b 4 ) 2 = ( 2 a ) 2 + ( 2 b ) 2 = 2 a 2 + b 2 = 1 0
Example that 10 is possible is to choose midpoints of segments of rectangle, or to put two points into one vertex and other two into opposite vertex.