Rectangle of the Year
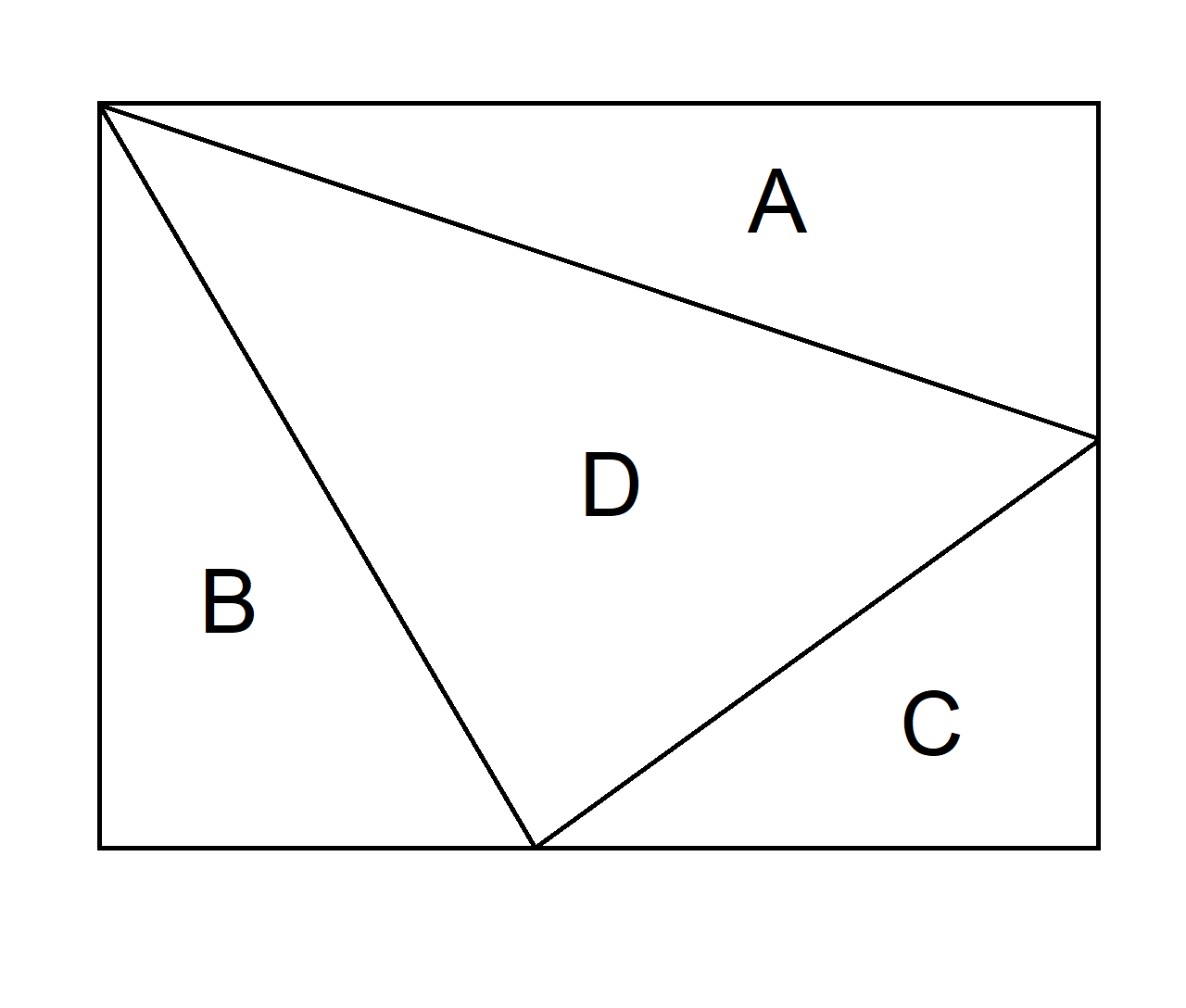
A rectangle is divided into four triangles with areas A , B , C , D , as shown.
If the rectangle's area is 2018, will A , B , C , D all be integers?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
If you factor 2 0 1 8 , you get 2 ⋅ 1 0 0 9 .
For all areas to be integers, the triangles A and B have to both have at least one even length leg.
If the height of B is 2, then the base of A is 1009 and the height of A is 1, so A does not have integer area.
The same argument applies if the base of A is 2, in which case the height of B is 1009 and base of B is 1, leaving B with non-integer area.
So A and B can't both have an integer area at the same time making it impossible for all the areas to be integers.
This is the approach I took. I assumed that the values of A, B, C, and D were integers, to begin with, and then used proof by contradiction to prove that this can not be the case. Here is my solution:
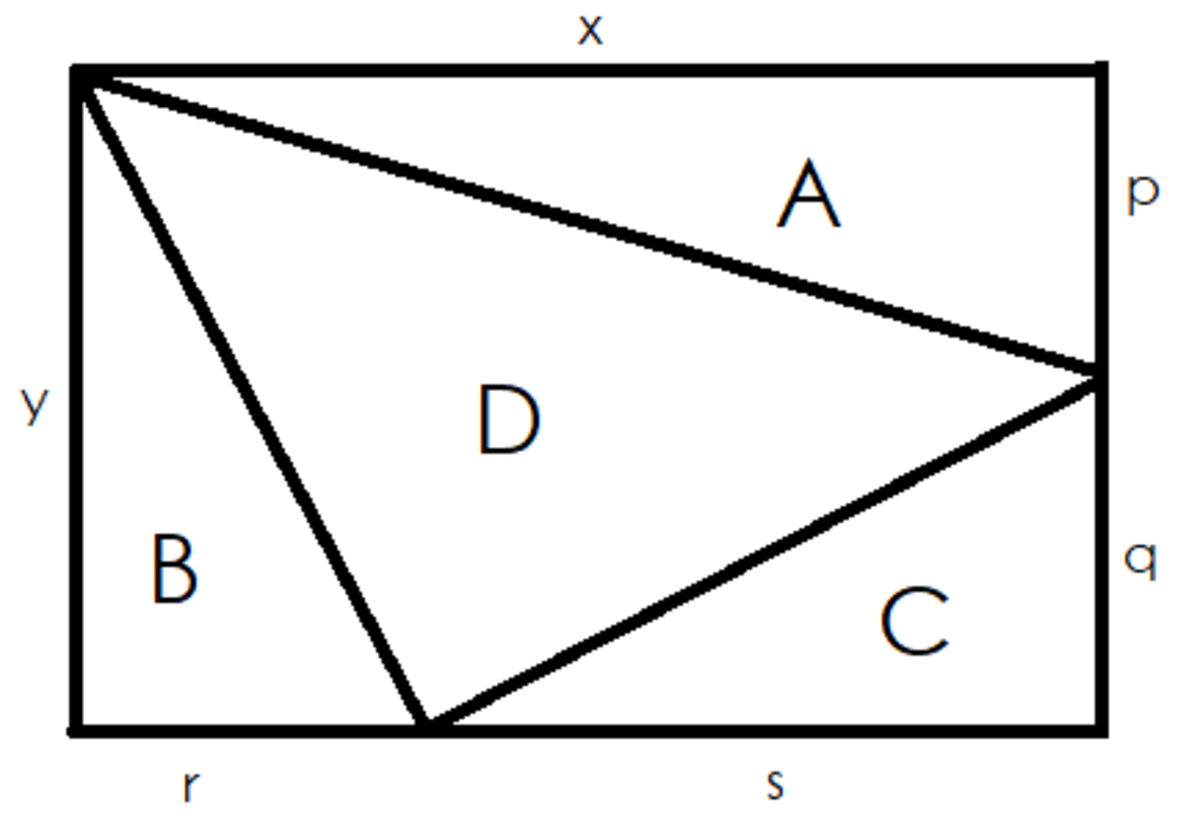
2 0 1 8 = 2 × 1 0 0 9 , meaning that ( x , y ) = ( 1 0 0 9 , 2 ) or vice versa. From the picture I drew, p + q = 2 and r + s = 1 0 0 9 .
A r e a ( B ) = ( y × r ) / 2 , but since y is a prime number, the only way for B to be an integer is for r to be divisible by 2 or in other words, even.
If r is even, then s is must clearly be odd.
A r e a ( C ) = ( q × s ) / 2 , and for C to be an integer, q must be even.
However, that can't be true, especially since p + q = 2 where q must be a member of the positive integers less than 2 and greater than 0. Having q being a member of the positive reals won't help either since then the area of C will end up not being an integer.
We have a contradiction meaning A , B , C , D can not all be integers!
the statement only tells us that A,B,C,D are integers. you can't assuming x and y are integers, it's possible x, y are any positive real number.
We can use proof by contradiction. Assume that A , B , C , and D are all integers. Let the horizontal side of the rectangle be a , the vertical side of the rectangle be b , the horizontal leg of triangle C be e , and the vertical leg of triangle C be f . We can see that e f = 2 C , ( a − e ) b = 2 B , and ( b − f ) a = 2 A . Multiplying the second and third equations together gives us a b ( a b − a f − e b + e f ) = 4 A B Adding the second and third equations together tells us that − a f − e b = 2 A + 2 B − 2 a b . Substituting this and the first equation into our other formula gives us a b ( a b + 2 A + 2 B − 2 a b + 2 C ) = 4 A B ⟹ ( a b ) 2 + ( − 2 A − 2 B − 2 C ) a b + 4 A B = 0 ⟹ a b = A + B + C ± ( A + B + C ) 2 − 4 A B We know that a b = A + B + C + D , so this simplifies to D 2 + 4 A B = ( A + B + C ) 2 ⟹ D 2 + 4 A B = ( 2 0 1 8 − D ) 2 ⟹ D = 1 0 0 9 − 1 0 0 9 A B . D must be an integer and 1 0 0 9 is prime, so A or B must be a multiple of 1 0 0 9 . 2 0 1 8 or any larger multiples couldn't satisfy A + B + C + D = 2 0 1 8 , so we can set A = 1 0 0 9 . This implies C = 0 which is a contradiction because C must be positive. Thus we know that A , B , C , and D cannot all be integers.