Rectangle on a Parabola
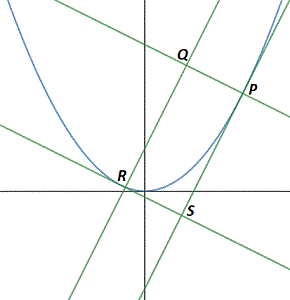 If
P
and
R
are points on the parabola
y
=
x
2
such that their tangents and normals form a rectangle
P
Q
R
S
that has a length that is twice as long as its width, then the area of that rectangle is
b
a
, where
a
and
b
are relatively primes. Find
a
+
b
.
If
P
and
R
are points on the parabola
y
=
x
2
such that their tangents and normals form a rectangle
P
Q
R
S
that has a length that is twice as long as its width, then the area of that rectangle is
b
a
, where
a
and
b
are relatively primes. Find
a
+
b
.
The answer is 253.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Great concept ! I'll borrow it soon...
Let P ( t , t 2 ) , R ( u , u 2 ) be the given points on the parabola. Then position coordinates of S are ( 2 t + u , t u ) .
Tangents at P and R are mutually perpendicular ⟹ t u = − 4 1
∣ P S ∣ = 2 ∣ R S ∣ ⟹ t 2 − 4 u 2 = 4 3
⟹ t 2 − 4 t 2 1 = 4 3 ⟹ 4 t 4 − 3 t 2 − 1 = 0
⟹ t = 1 , u = − 4 1 , ∣ P S ∣ = 8 5 5 .
So, the area of the rectangle is 2 1 × ∣ P S ∣ 2 = 1 2 8 1 2 5
Hence a = 1 2 5 , b = 1 2 8 , a + b = 2 5 3 .
Can you show more steps on how you knew the position coordinates of S are ( 2 t + u , t u ) ? Thanks.
The point S has to be at the intersection of the lines < t , t 2 > + α < 1 , 2 t > and < u , u 2 > + β < 1 , 2 u > . Making the two vectors equal and solving the corresponding system of equations for α and β , you can obtain that α = 2 1 ( u − t ) and β = 2 1 ( t − u ) . Then you get the coordinates of S , for example, by replacing β = 2 1 ( t − u ) into the vector < u , u 2 > + β < 1 , 2 u > .
Let the coordinates of P be ( p , p 2 ) and R be ( r , r 2 ) . Without loss of generality, let p > 0 , r < 0 , and P S = 2 R S .
Then the tangent line through P is y = 2 p x − p 2 and the tangent line through R is y = 2 r x − r 2 .
As sides of a rectangle, the two tangent lines must be perpendicular, so 2 p ⋅ 2 r = − 1 , or r = − 4 p 1 . Therefore, the coordinates of R are ( − 4 p 1 , 1 6 p 2 1 ) and the tangent line through R is y = − 2 p 1 x − 1 6 p 2 1 .
The coordinates of the intersection of the two tangent lines at S is then ( 8 p 4 p 2 − 1 , − 4 1 ) .
By the distance equation, P S = 8 p ( 4 p 2 + 1 ) 3 and R S = 1 6 p 2 ( 4 p 2 + 1 ) 3 .
Since P S = 2 R S , 8 p ( 4 p 2 + 1 ) 3 = 2 ⋅ 1 6 p 2 ( 4 p 2 + 1 ) 3 , which solves to p = 1 for p > 0 .
The area of the rectangle is A P Q R S = P S ⋅ R S = 8 p ( 4 p 2 + 1 ) 3 ⋅ 1 6 p 2 ( 4 p 2 + 1 ) 3 = 1 2 8 p 3 ( 4 p 2 + 1 ) 3 . Since p = 1 , A P Q R S = 1 2 8 ⋅ 1 3 ( 4 ⋅ 1 2 + 1 ) 3 = 1 2 8 1 2 5 .
Therefore, a = 1 2 5 , b = 1 2 8 , and a + b = 2 5 3 .