Rectangles Are Cool!
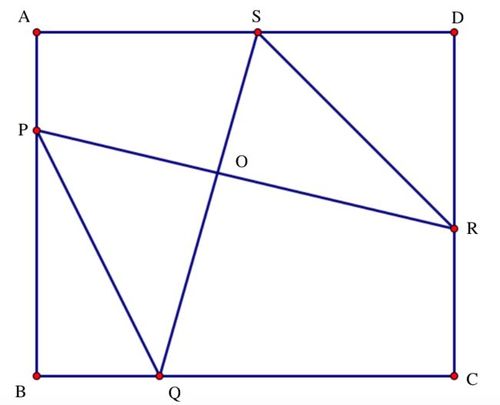 In the figure above,
A
B
C
D
is a rectangle,
P
B
=
1
0
cm
,
A
S
=
8
cm
,
Q
C
=
1
2
cm
,
D
R
=
8
cm
. The area of the triangle
P
O
Q
and triangle
O
S
R
are both
3
0
cm
2
. And
O
is the intersection point of the straight lines
P
R
and
Q
S
. Find the area of the rectangle
A
B
C
D
(in
m
2
).
In the figure above,
A
B
C
D
is a rectangle,
P
B
=
1
0
cm
,
A
S
=
8
cm
,
Q
C
=
1
2
cm
,
D
R
=
8
cm
. The area of the triangle
P
O
Q
and triangle
O
S
R
are both
3
0
cm
2
. And
O
is the intersection point of the straight lines
P
R
and
Q
S
. Find the area of the rectangle
A
B
C
D
(in
m
2
).
Credits to my math teacher for coming up with this problem.
The answer is 0.0238.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Why on earth would all the dimensions be given in c m , and then the answer in m 2 be asked for??
To trick the solver :)
Log in to reply
It worked on me.
Log in to reply
Yes to start with I knew it was in meter. But while giving answer I too forgot !!
@eugene, your math teacher didn't say the answer is in m square...
O (6.8, 8.4) with h = 5 and k = 4 added as (10 + 4)(5 + 12) = 238 c m 2
0 . 1 4 × 0 . 1 7 = 0 . 0 2 3 8 ( m 2 )
Answer: 0 . 0 2 3 8
How did u get the coordinates of point O?
It is sufficient to know that the area of the triangles are equal, I didn't use the number 30:
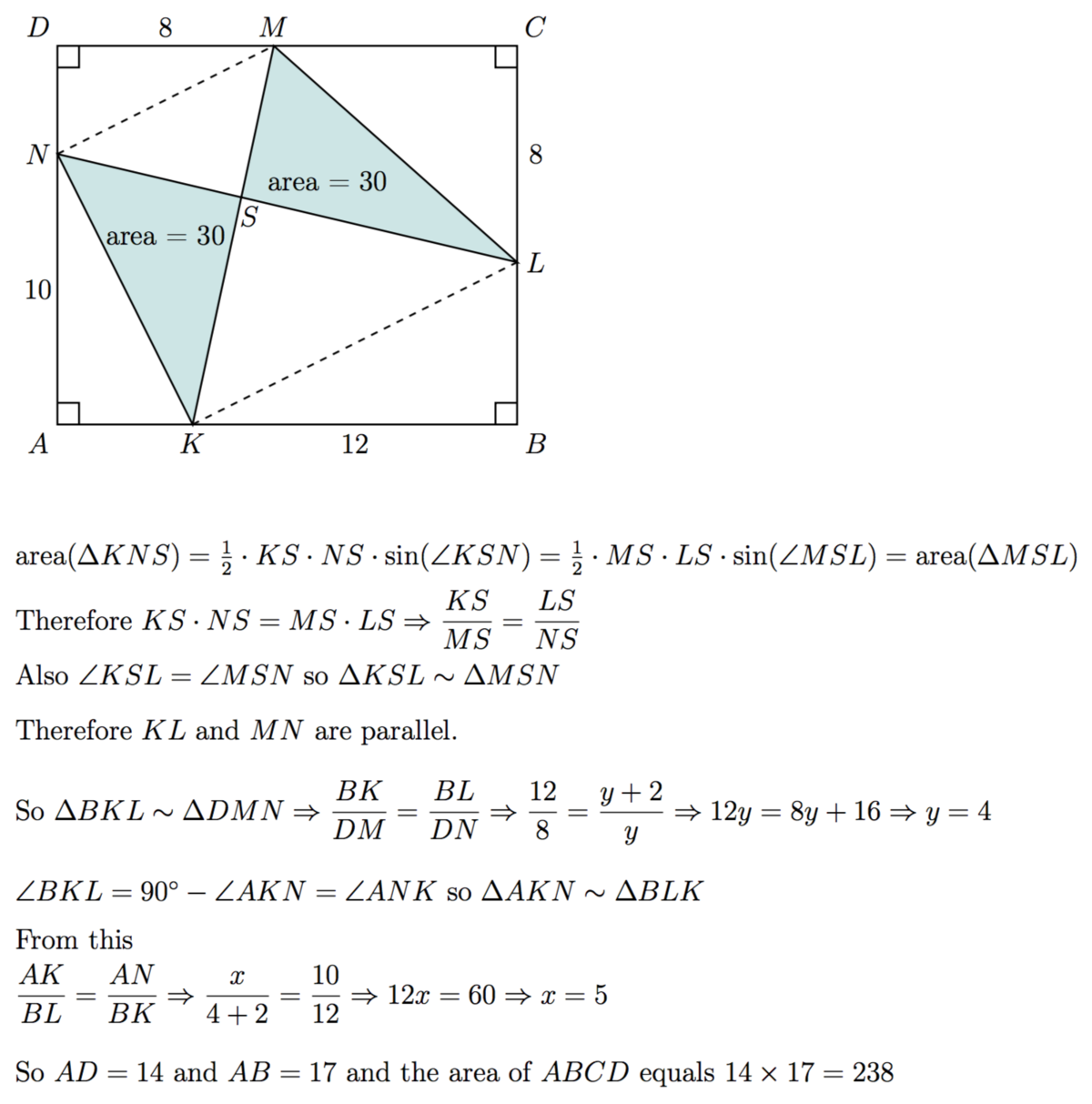
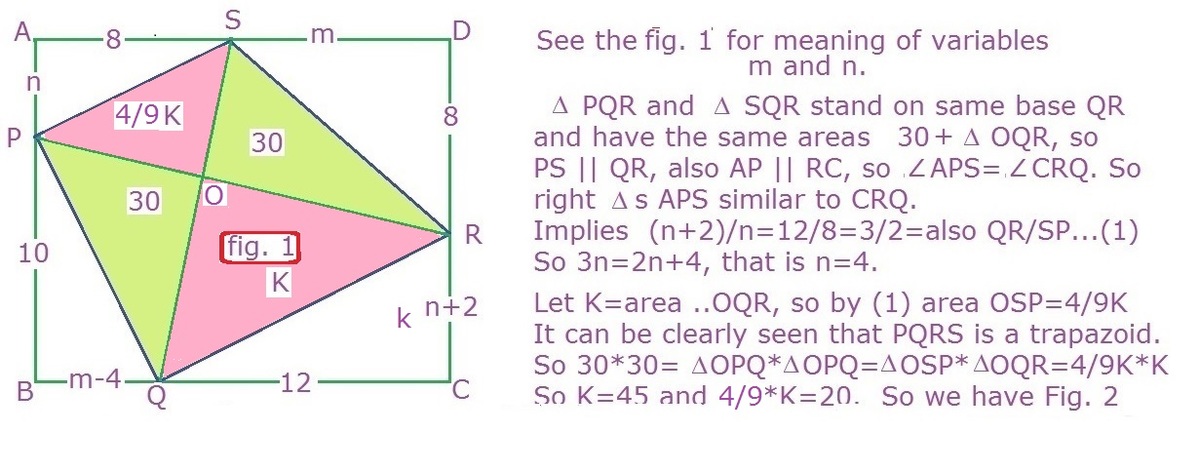
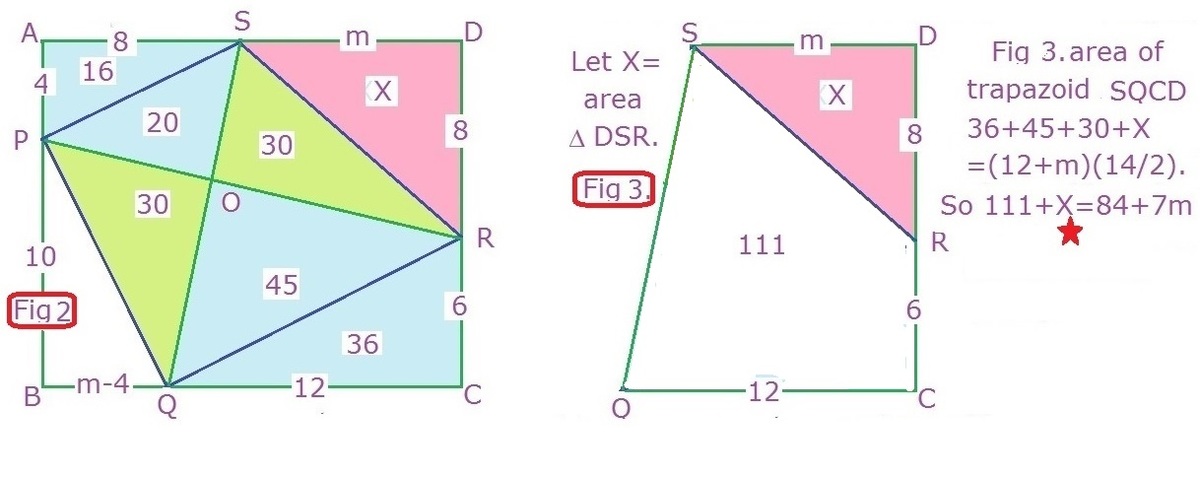
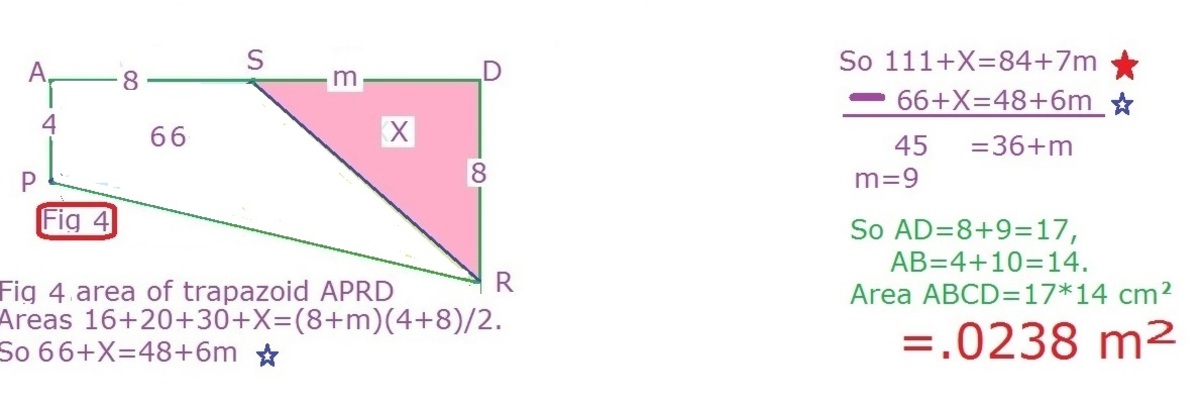
The solution is too long for me to write so I have uploaded the pics which show the solution of this problem,I would like someone else to come up with a more simpler and elegant way of the solution to this question. Please be free to ask if you don't understand any part of my approach!