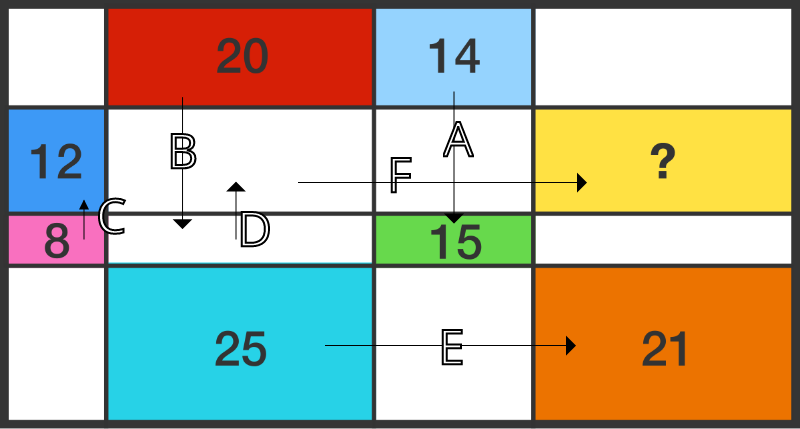
Rectangles in rectangle
A rectangle is divided into 16 smaller rectangles, the areas of seven of which are known to us by the numbers in the figure (which is not drawn to scale).
What is the area of the yellow rectangle?
The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Nice and elegant solution!
For a complete solution you'd probably want a few words to justify the substitutions for (b/c), (a/d) and (c/a). I mean, yeah, it's mostly obvious.
My approach was similar but I used ratios of column widths instead of ratios of row heights.
Can we assume they're the same width, given it's not drawn to scale? I couldn't advance on this question at all because I didn't know if I could make the assumption that the columns and rows were marked consistently.
Log in to reply
All are rectangles and all lines are parallel. All rectangles in a row have the same height and all rectangles in a column have the same width.
Let x 1 , x 2 , x 3 , x 4 and y 1 , y 2 , y 3 , y 4 the respective horizontal and vertical lengths of the rectangles. As an example, the red square has area x 2 ∗ y 1 . The following holds :
x 1 ∗ y 2 x 1 ∗ y 3 x 2 ∗ y 1 x 2 ∗ y 4 x 3 ∗ y 1 x 3 ∗ y 3 x 4 ∗ y 4 x 4 ∗ y 2 = = = = = = = = 1 2 8 2 0 2 5 1 4 1 5 2 1 ?
The game is now to multiply and divide terms to get to x 4 ∗ y 2 . The only one with x 4 is the orange square so we start with x 4 ∗ y 4 and remove y 4 by dividing by the 4th row. Then, we repeat the process.
There is only one possibility (life is beautiful), leading to x 4 ∗ y 2 : ( x 4 ∗ y 4 ) 2 1 ∗ / ( x 2 ∗ y 4 ) − 1 2 5 ∗ ∗ ( x 2 ∗ y 1 ) 2 0 ∗ / ( x 3 ∗ y 1 ) − 1 1 4 ∗ ∗ ( x 3 ∗ y 3 ) 1 5 ∗ / ( x 1 ∗ y 3 ) − 1 8 ∗ ∗ ( x 1 ∗ y 2 ) 1 2 = = x 4 ∗ y 2 2 7
They don't say they are straight lines. X1 might be different for the first square than for the second.
The reason ur all wrong is the square 25, it says THERE ALL rectangles. Length times width. The number would have a decimal in it.
Log in to reply
There is no reason that the width or height is not allowed to be a decimal. Actually, in this problem, the width or height could be anything. The area is calculable, though, and it just happens to be an integer.
Considering the two rectangles with known areas in the topmost row, they have areas in the ratio 1 4 2 0 = 7 1 0 . In other words, the rectangle immediately to the right of the one with area 25 has area 7 1 0 2 5 = 7 2 5 = 5 × 2 7 = 2 5 × 7 = 2 3 5 .
Next considering the two rectangles with areas 8 and 15, the rectangle immediately below the one with area 8 has area 1 5 8 × 2 3 5 = 3 4 × 7 = 3 4 × 7 = 3 2 8 .
Finally considering this rectangle with area 3 2 8 and the one with area 21, they have areas in the ratio 2 1 3 2 8 = 3 3 4 = 3 × 3 4 = 9 4 . Then considering the rectangle with area 12, the unknown area would be 9 4 1 2 = 1 2 × 4 9 = 4 1 2 × 9 = 3 × 9 = 2 7
Similar to Noel, I just re-drew the matrix and started filling in empty boxes by writing out the corresponding ratios from known pairs to an empty box with half its pair revealed. I simplified fractions but left them in fractional form, which made computation easier in the end. If rows are a, b, c, d top to bottom and columns are 1, 2, 3, 4 left to right, I started with box d3, noting the ratio of d2 to a2 was 5/4, so d3 would be 5/4*14 or 35/2.
Also, since ratio b1 to c1 is 3/2, b3 is 3/2*15 (c3 value) or 45/2.
Ratio of b3 top d3 is 45/2: 35/2 or 9/7. therefore b4 (value sought) is 9/7 of d4, or 9/7*21 = 27
@Chew-Seong Cheong provided a solution based on the height of rows. An entirely analogous solution can be given based on the width of columns. Let p , q , r , s be the widths for the columns, from left to right, and x the unknown area. Then ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ q s = 2 5 2 1 r q = 1 4 2 0 = 7 1 0 p r = 8 1 5 p s = 1 2 x . Since p s = q s ⋅ r q ⋅ p r , we have 1 2 x = 2 5 2 1 ⋅ 7 1 0 ⋅ 8 1 5 = 4 9 , so that x = 1 2 ⋅ 4 9 = 3 ⋅ 9 = 2 7 .
Looking at column 2: C2 * R1 = 20 C2 * R4 = 25 So that's easy, the common factor is 5, so: C2 = 5 R1 = 4 R4 = 5 The rest is inevitable! C4 = 21 ÷ 5 = 4 1/5 (or 4.2) C3 = 14 ÷ 4 = 3 1/2 (or 3.5) R3 = 15 ÷ 3 1/2 = 4 2/7 (which is why I prefer to work with fractions!) C1 = 8 ÷ 4 2/7 = 28/15 = 1 13/15 (just less than two, sounds about right!) R2 = 12 ÷ 28/15 = 45/7 = 6 3/7 So the area of our mystery box will be: C4 * R2 = 4 1/5 * 6 3/7 = 21/5 * 45/7 - which reduces very nicely! 3/1 * 9/1 = 3 * 9 = 27 Q.E.D. (all of which was very nicely formatted until I hit the "Publish" button!)
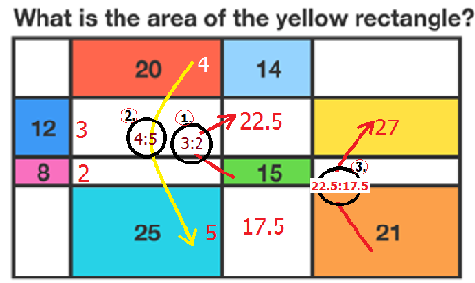
I don't understand your explanation. What does all the "4:5" , "3:2" , "22.5 :17.5" represent?
This one is really challenging to do mentally. So, we can apply a little trick!

b a = B A
All the bold edge is doing is multiplying both a and b by the same constant.
This was the toughest part to get. Now, we will build up the calculation using that diagram:
2 0 × 1 4 1 5 × 8 1 2 × 2 5 2 1 = x
We can simplify a bit :
2 0 × 1 4 1 5 × 2 3 × 2 5 2 1 = x
Then further :
2 0 × 2 1 5 × 2 3 × 2 5 3 = x
And again
2 0 × 2 3 × 2 3 × 5 3 = x 4 × 2 3 × 2 3 × 3 = x 3 × 3 × 3 = x
And finally: 2 7 = x
So, we have found our target: 27 .
This looks very neat. For clarity, it would be helpful to explain what "x" represents.
Let X1,X2,X3,X4 and Y1,Y2,Y3,Y4 the respective horizontal and vertical lengths of the rectangles
Here is a shorter solution We have
21 * 20 * 12 * 15 = product of all small edges = X1 * X2 * X3 * X4 * Y1 * Y2 * Y3 * Y4
We also have 12 * 8 * 20 * 25 * 14 * 15 * 21 * orange area = (product of all small edges) ^2 Therefore Orange Area = (21 * 20 * 12 * 15)^2 / (12 * 8 * 20 * 25 * 14 * 15 * 21) = 27
Nice. "Multiplying every side lengths" somehow leads us to the desired answer.
Area of rectangle above yellow.
=(21/25)(20)=84/5,
Area of White rectangle below yellow.
=(15/14)(84/5)=18,
Area of yellow=(18/8)(12)=27
I don't understand. How did you get 21/25 and 20? And how did you get 15/14 and 84/5?
Let heights of top row to the bottom row be a , b , c and d respectively and the unknown area of yellow rectangle be x . Since rectangle in the same column have the same width, their areas are directly proportional to their heights. For example, in the first column, rectangle in the second and third rows c b = 8 1 2 . The same for other columns. Therefore, we have:
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ c b = 8 1 2 = 2 3 d a = 2 5 2 0 = 5 4 c a = 1 5 1 4 d b = 2 1 x … ( 1 ) … ( 2 ) … ( 3 ) … ( 4 )
From (4):
d b ⟹ x = 2 1 x = 2 1 × d b = 2 1 × c b × d a × a c = 2 1 × 2 3 × 5 4 × 1 4 1 5 = 2 7