Rectangular Mystery
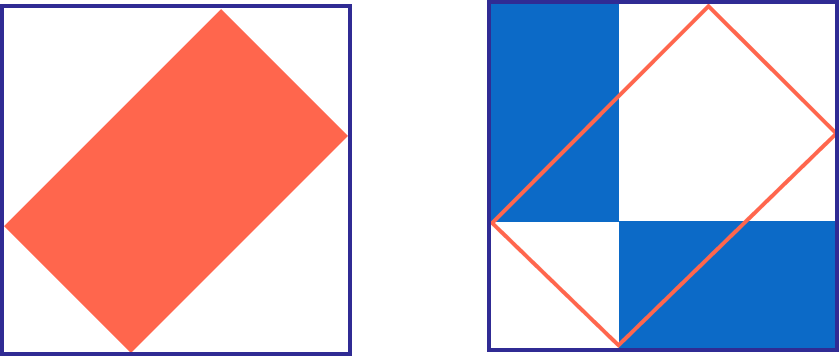
On the left diagram above, the red rectangle is inscribed in a larger outside rectangle.
On the right, in the same outside rectangle, two blue rectangles are formed by the perpendicular lines arising from 2 adjacent vertices of the red rectangle.
Which one has a larger area, the red region or the blue region?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Already edited. Thank you for your advice.
By definition, all angles in a rectangle are right angles.
Or, just use the property that area of triangles on the same base and between the same parallels are equal.
This problem was so easily solved without using the Cauchy-Schwarz inequality. I did it in a similar way, and was wondering what it was doing here in this wiki. Hmmm.
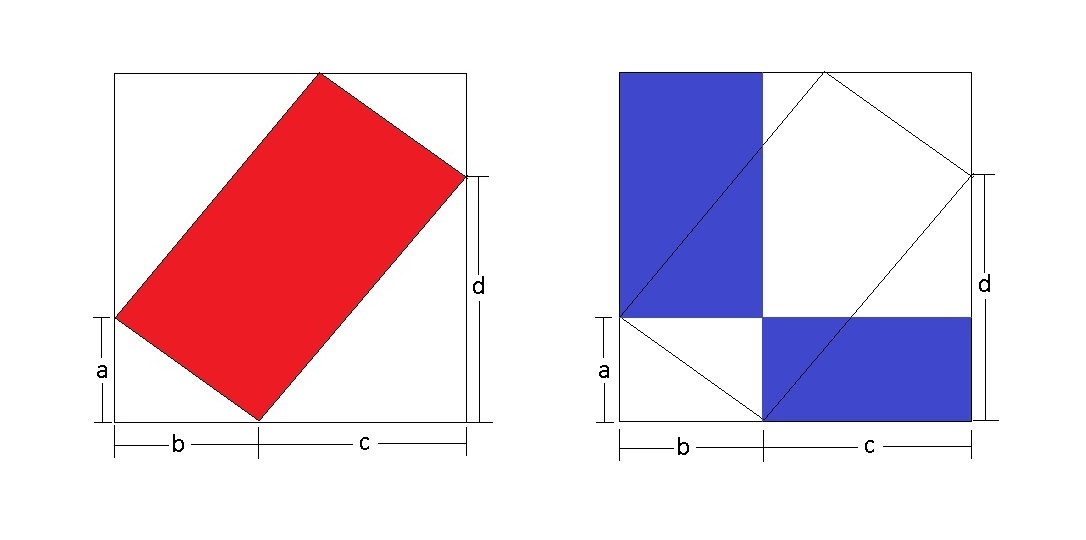
Let a , b , c , d be the lengths of the segments as shown above.
By using Pythagorean theorem, it is obvious that the red rectangular area = ( a 2 + b 2 ) ( c 2 + d 2 ) .
Then the blue rectangular area = a c + b d .
According to Cauchy-Schwarz Inequality , for the 2 terms inequality, ( a 2 + b 2 ) ( c 2 + d 2 ) ≥ ( a c + b d ) 2 .
Taking square root on both sides, we will get ( a 2 + b 2 ) ( c 2 + d 2 ) ≥ ( a c + b d ) .
This inequality becomes equation when b a = d c and in this case, the smaller and the bigger white triangles enclosing the red area are similar due to right angle complementation. Hence, it corresponds to this condition.
As a result, the red area = the blue area.
Moderator note:
The way your solution is written, it is confusing to the reader because it sets them up with the expectation that you are proving the red area >= blue area.
The way your solution is written, it is confusing to the reader because it sets them up with the expectation that you are proving the red area >= blue area.
Log in to reply
That's what I intended actually, but then Mr. Mendrin corrected the solution. So I had to adapt it to be equality.
This can be done visually. In the first image join the long sides of the two large white triangle to form a rectangle. Then do the same for the two small white triangles.Push these two rectangles to opposite corners of the square and you will obtain the second image, thus showing that the white area is equal in both. it follows that the coloured areas are also equal.
WLOG assume the inner rectangle is a square.
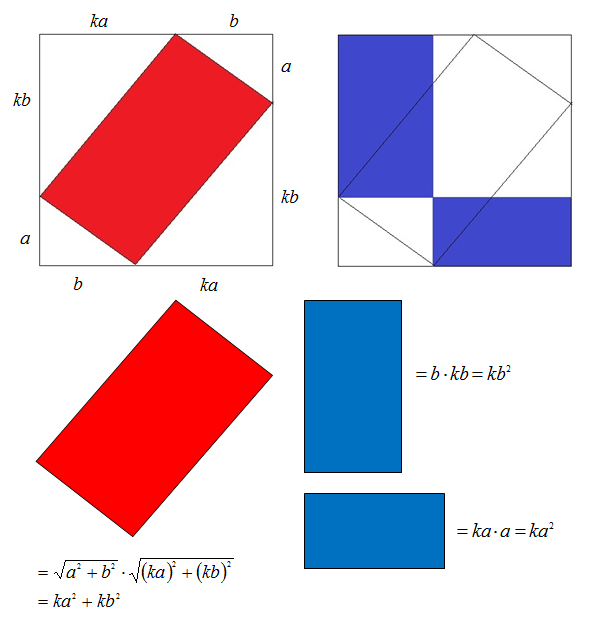
Relevant wiki: Length and Area - Composite Figures
Using the graphic provided in Worranat's solution:
the area of the whole rectangle is ( a + d ) ( b + c ) , so that the area of the red rectangle is ( a + d ) ( b + c ) − a b − c d = a c + b d . The combined area of the blue rectangles is a c + b d . Hence they are always the same. This assumes that b a = d c so that the red figure is a rectangle with right angled corners.