Rectangular prisms!
Given a rectangular prism (as shown below) whose edge lengths have a sum of 36, what is the minimum value for the length of the line connecting two vertices which do not share a face?
If the minimum value can be expressed as a b , where a and b are integers with b square-free, submit your answer as a + b .
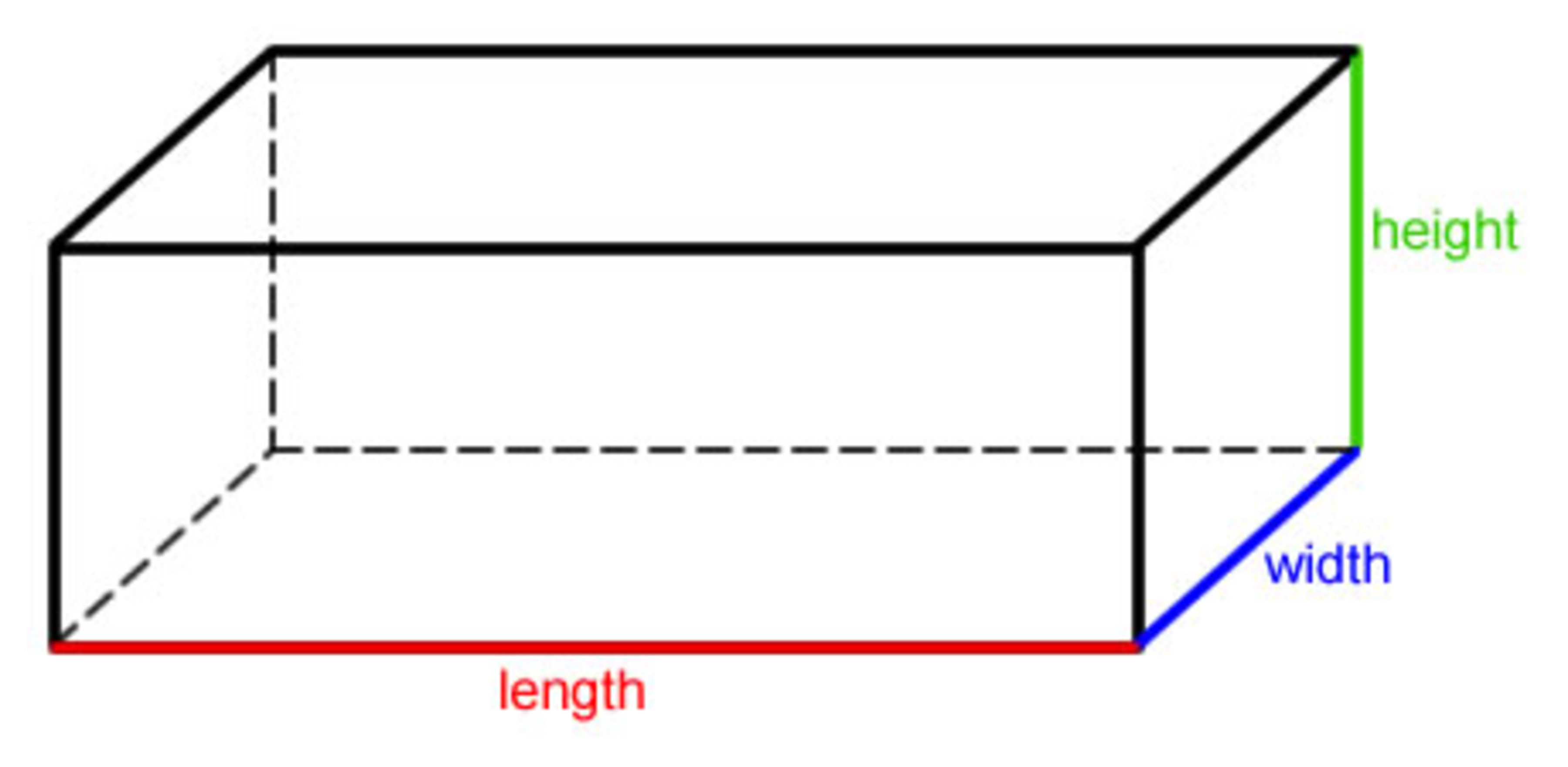
Image credit: http://dooleymath.com/
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution! It would be better if you show that equality can be attained (when x = y = z = 3 ).
My approach was not really the intended one, it uses the rearrangement inequality instead.
Let the width, length, and height of the prism be x , y , and z . Since 4 x + 4 y + 4 z = 3 6 , x + y + z = 9 .
Square both sides to get x 2 + y 2 + x 2 + 2 ( x y + y z + z x ) = 8 1 .
Moving things, we get x y + y z + z x = 2 8 1 − ( x 2 + y 2 + z 2 ) .
From the Rearrangement Inequality, x 2 + y 2 + z 2 ≥ x y + y z + z x .
So, x 2 + y 2 + z 2 ≥ 2 8 1 − ( x 2 + y 2 + z 2 ) .
3 ( x 2 + y 2 + z 2 ) ≥ 8 1
x 2 + y 2 + z 2 ≥ 2 7
x 2 + y 2 + z 2 ≥ 3 3
This is obtainable when x = y = z = 3 .
This is actually a direct application of the Power Mean Inequality.
Let the height, width and length of the prism be x , y , z respectively. The sum of all edge lengths is given as 2 x + 2 y + 2 y + 2 z + 2 x + 2 z = 4 x + 4 y + 4 z , since there are four of each edge in the prism.
Since 4 x + 4 y + 4 z = 3 6 , we get that x + y + z = 9 , and what we are asked for is the smallest possible length of a diagonal, which is x 2 + y 2 + z 2 . By the power mean inequality, we get 3 x 2 + y 2 + z 2 ≥ 3 x + y + z = 3 9 = 3 . Multiplying both sides by 3 gives us x 2 + y 2 + z 2 ≥ 3 3 , so we get a = b = 3 . Our answer is then a + b = 3 + 3 = 6 .