Rectangular Pyramid
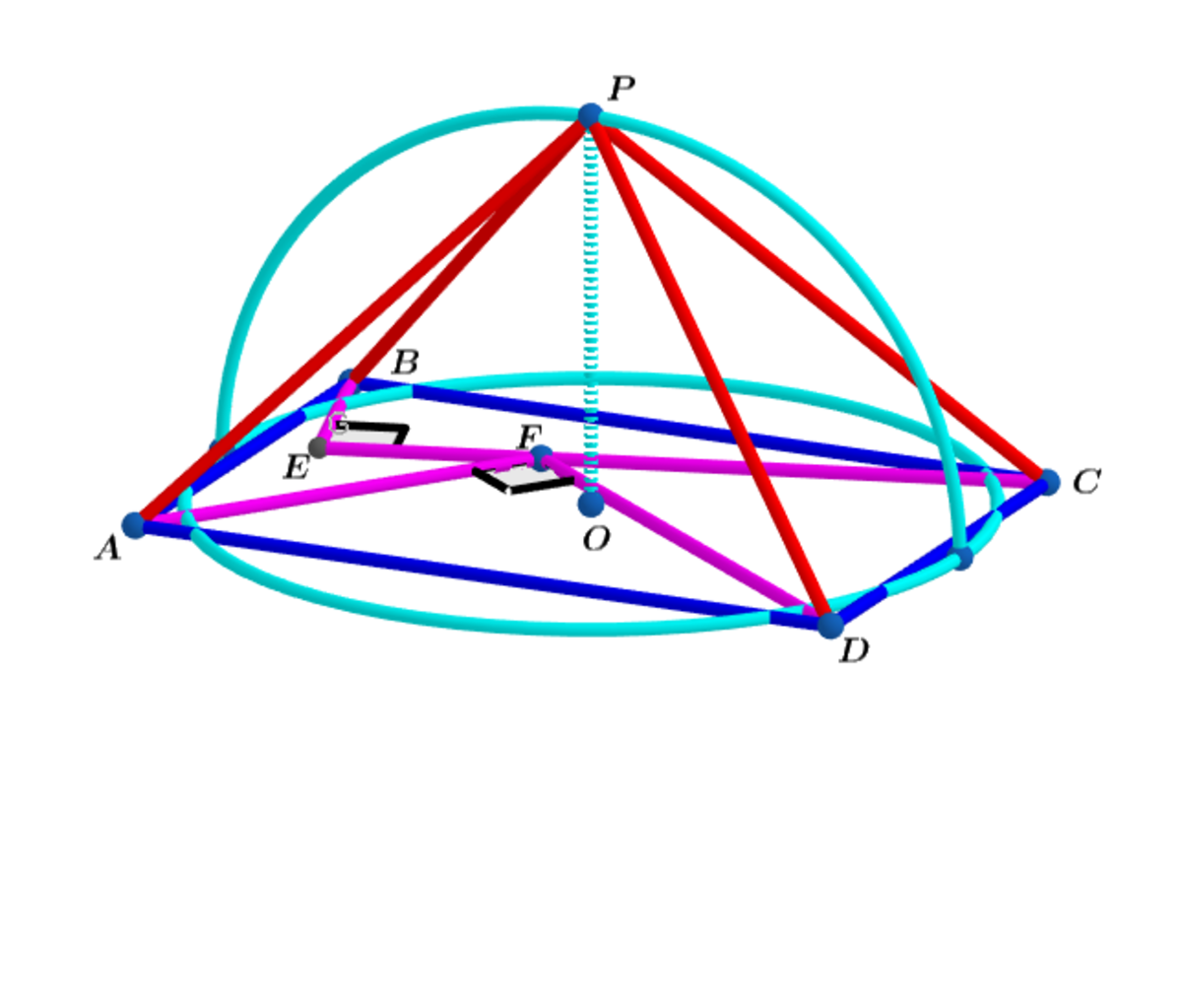
Inside rectangular base A B C D , △ B E C and △ A F D are right triangles and F lies on E C , where B E = 7 , E C = 2 4 and A F = 1 5 .
Let O be the center of rectangle A B C D and construct a circle centered at O whose circumference is equal to the perimeter of the rectangle. Folding the arc of the semi-circle at a right angle, as shown above, the radius of the semicircle becomes the height of the rectangular pyramid.
Find the total surface area of the rectangular pyramid.
The answer is 1112.00931858.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
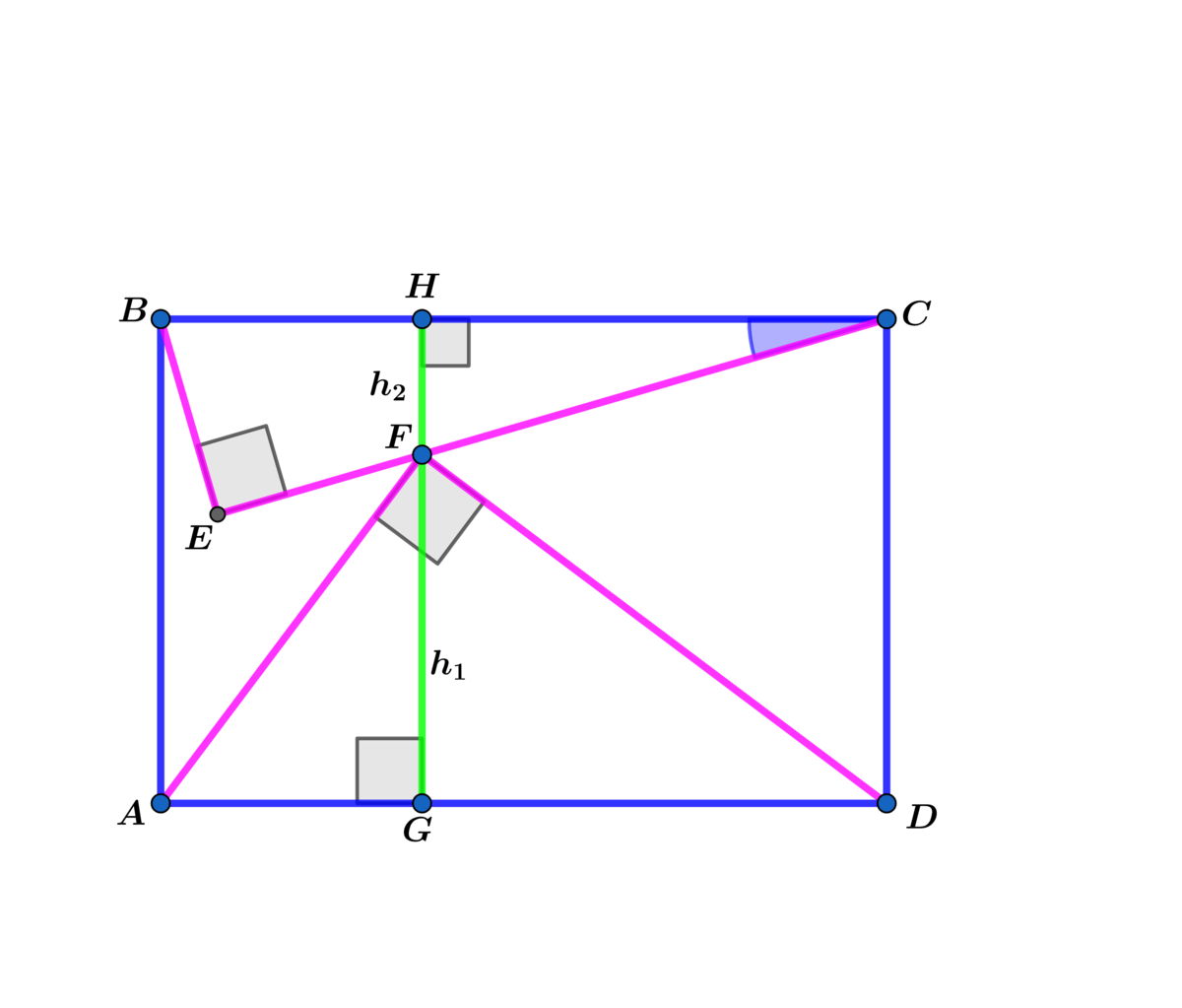
Let B E = 7 , E C = 2 4 and A F = 1 5 .
B C = A D = 7 2 + 2 4 2 = 6 2 5 = 2 5 and 2 2 5 = 2 5 ∗ A G ⟹ A G = 9
⟹ G D = H C = 1 6 ⟹ h 1 = 1 5 2 − 9 2 = 1 4 4 = 1 2
△ B E C ∼ △ H F C ⟹ h 2 7 − 1 6 2 4 ⟹ h 2 = 3 1 4 ⟹
A B = C D = 1 2 + 3 1 4 = 3 5 0 ⟹ A A B C D = 2 5 ( 3 5 0 ) = 3 1 2 5 0
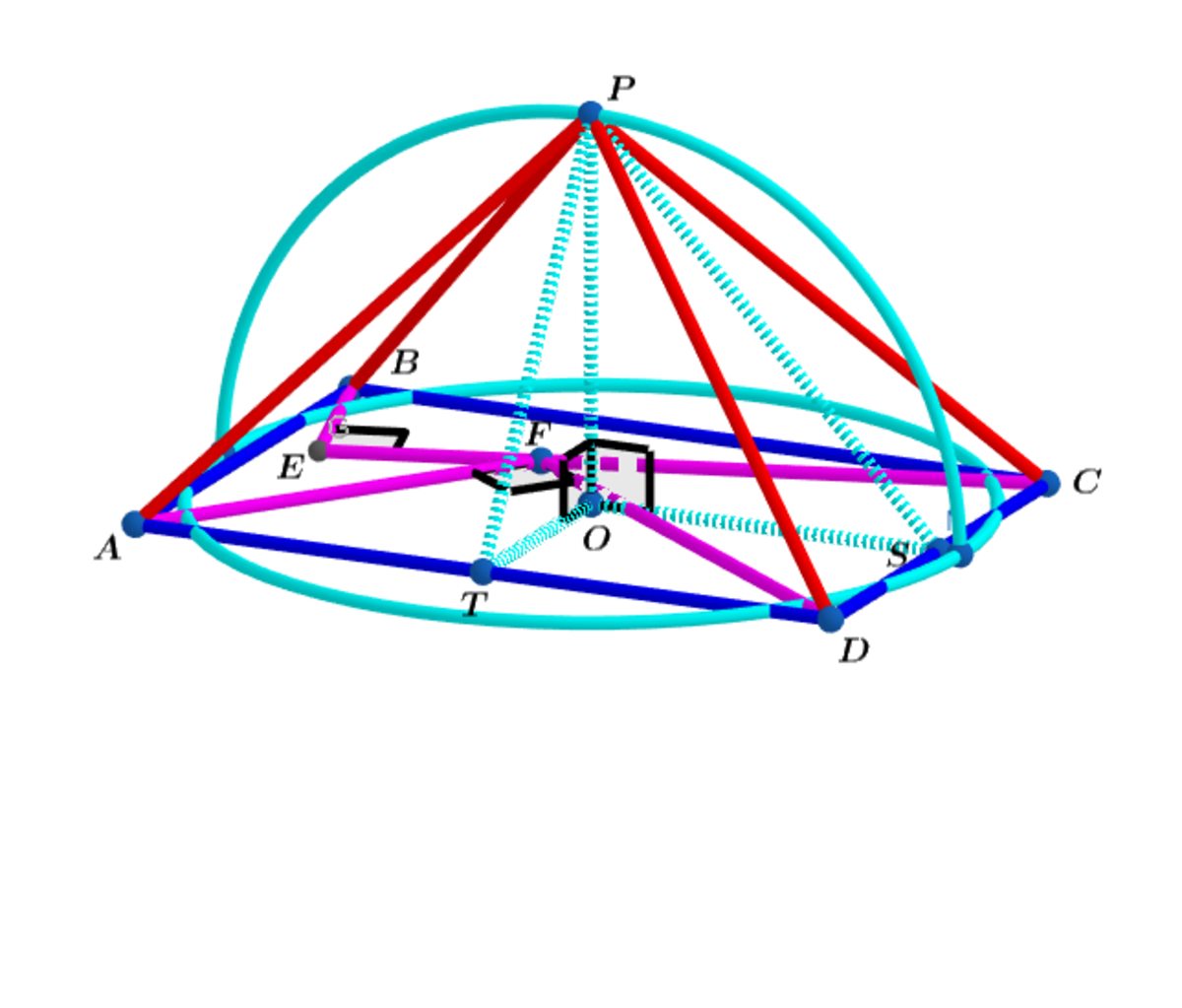
The perimeter P = 5 0 + 3 1 0 0 = 3 2 5 0 = 2 π r ⟹ r = 3 π 1 2 5 = O P
O T = 3 2 5 and O S = 2 2 5 and O P = 3 π 1 2 5 ⟹
P T = 3 π 2 5 π 2 + 2 5 and P S = 6 π 2 5 9 π 2 + 1 0 0 ⟹
The total surface area A = 3 1 2 5 0 + 3 π 6 2 5 π 2 + 2 5 + 9 π 6 2 5 π 2 + 1 0 0 =
9 π 6 2 5 ( 6 π + 3 π 2 + 2 5 + 9 π 2 + 1 0 0 ) ≈ 1 1 1 2 . 0 0 9 3 1 8 5 8 .
Let ∠ F D C = ∠ F A D = α , ∠ F C D = ∠ C B E = β . Then ∣ B C ∣ = ∣ A D ∣ = 7 2 + 2 4 2 = 2 5 , ∣ F D ∣ = 2 5 2 − 1 5 2 = 2 0 , sin α = 2 5 2 0 = 5 4 ⟹ cos α = 5 3 , sin β = 2 5 2 4 ⟹ cot β = 2 4 7 . ∣ C D ∣ = ∣ F D ∣ × sin β sin ( α + β ) = 2 0 × ( cos α + cot β sin α ) = 3 5 0 . From the given condition, the height of the pyramid h is given by 2 π h = 2 ( 3 5 0 + 2 5 ) ⟹ h = 3 π 1 2 5 . Height of the triangle on base A D is ( 3 π 1 2 5 ) 2 + ( 3 2 5 ) 2 ≈ 1 5 . 6 6 3 6 , and on base C D is ( 3 π 1 2 5 ) 2 + ( 2 2 5 ) 2 ≈ 1 8 . 2 2 5 1 . Area of base = 2 5 × 3 5 0 ≈ 4 1 6 . 6 6 7 . Lateral surface area is 2 × 2 1 × 1 5 . 6 6 3 6 + 2 × 2 1 × 1 8 . 2 2 5 1 = 6 9 5 . 3 4 2 6 . Hence the total surface area is 4 1 6 . 6 6 7 + 6 9 5 . 3 4 2 6 = 1 1 1 2 . 0 0 9 3 .