Rectangular spiral
Starting at
(
0
,
0
)
, we draw line segment #1 of length
1
to the right; turning
9
0
∘
counterclockwise, we draw line segment #2 of length
2
1
upward; turning
9
0
∘
counterclockwise again, we draw line segment #3 of length
3
1
to the left; and so on: line segment #
n
has length
1
/
n
.
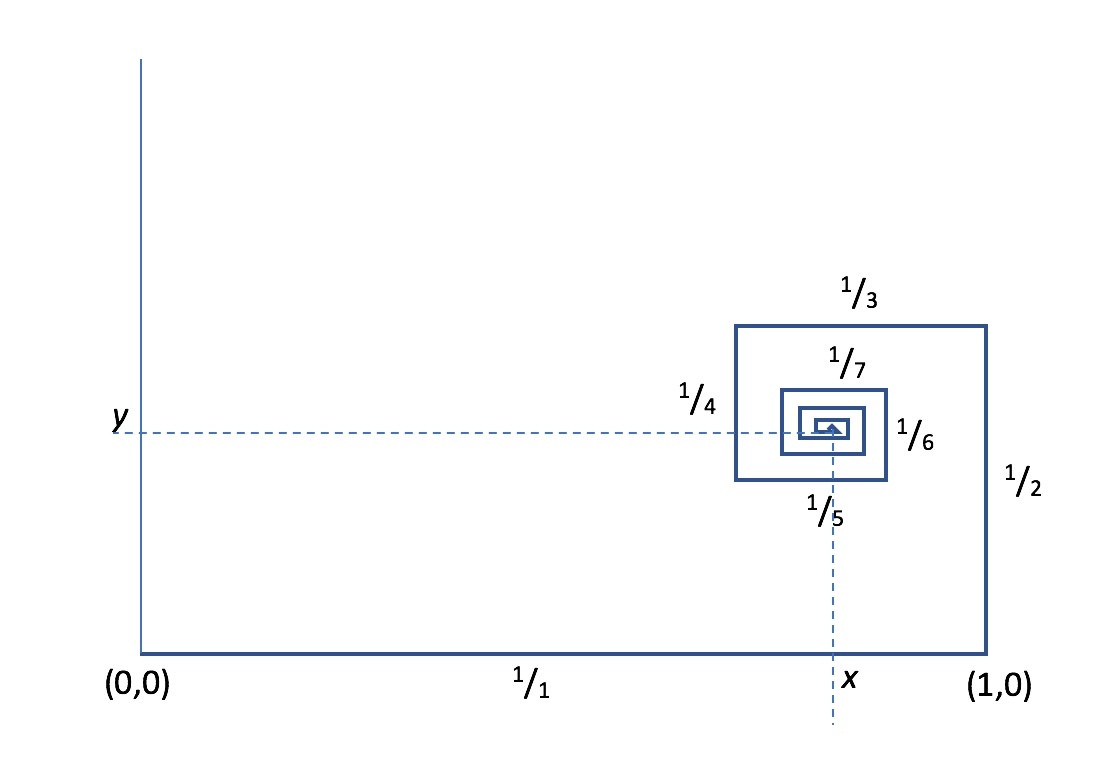 The spiral converges to point
(
x
,
y
)
.
The spiral converges to point
(
x
,
y
)
.
Characterize x and y by two digits, using the following code.
- 0 = rational number
- 1 = natural logarithm of a rational number
- 2 = natural logarithm of a square root of a rational number
- 3 = rational multiple of e
- 4 = rational multiple of π
- 5 = irrational square root of a rational number
- 6 = none of the above
For instance, if x is a rational multiple of e and y is the natural logarithm of a rational number, give your answer as 3 1 .
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This approach with complex numbers suggests a way to transform this rectangular spiral into a smooth curve, defining
z
t
=
∫
0
t
t
+
1
i
t
d
t
=
∫
0
t
exp
(
−
ln
(
t
+
1
)
+
2
π
t
i
)
d
t
.
The curve obtained in this way looks like this:
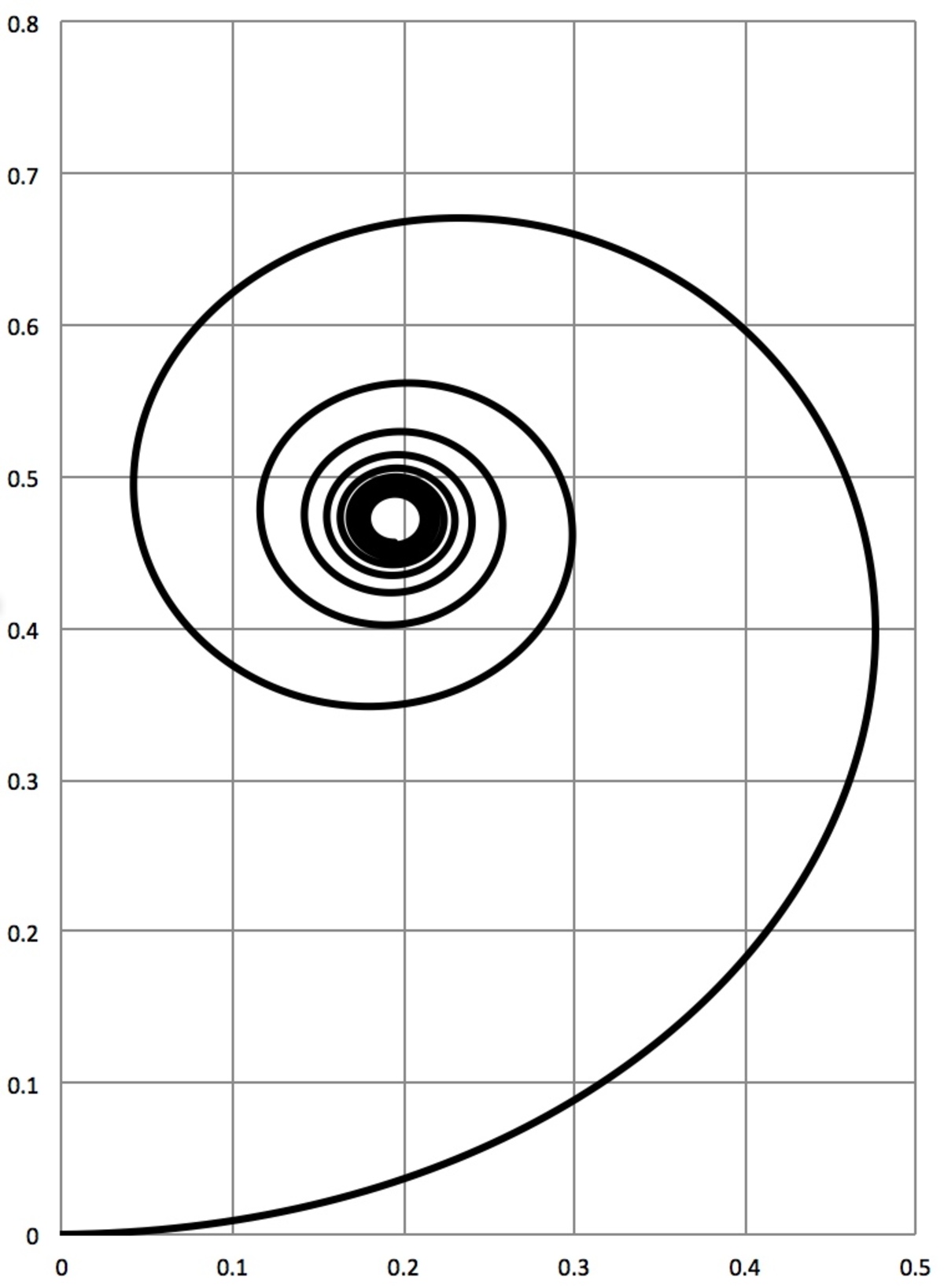 Its also converges, and also slowly... any idea to what point?
Its also converges, and also slowly... any idea to what point?
Your solution is brilliant! All encapsulated into one series. I would've never thought of that. I wonder if Arjen chose 42 on purpose btw. You know, "the answer to life, the universe and everything?"
I believe you meant pi/2 in the exponent, Arjen. How should I address you by the way?
Log in to reply
Thanks for being so observant, James. I'll fix that. "Arjen" is just fine, btw.
I have to go, but I'm going to attempt this one tomorrow.
So far I've gotten it down to solving the cos(x)/x and sin(x)/x integrals from pi/2 to infinity. I'm now working on finding the antiderivative of exp(bpi/2)b/(b^2+1).
Log in to reply
For ∫ ( cos x ) / x d x and ∫ ( sin x ) / x d x , see sine integrals , or Dirichlet integral .
Log in to reply
For sure. But I'm going to see what I can do on my own first. I'm a bit distracted right now. 4 people texting me.
Thanks for the links. I used integral-calculator.com to approximate the integrals and I got 0.20003 for the x-value and 0.47200 for the y-value. That's interesting, considering it's off-center from where the spiral looks like it's headed looking at your graph (unless that's due to roundoff error).
Log in to reply
I generated my graph using a simple numerical integration in Excel. The step-size was not super small, so there may well be some rounding error.
We have x = 1 − 3 1 + 5 1 − 7 1 + − ⋯ = 1 1 1 − 3 1 3 + 5 1 5 − 7 1 7 + − ⋯ = arc tg 1 = 4 π ≈ 0 . 7 8 5 4 ; and y = 2 1 − 4 1 + 6 1 − 8 1 + − ⋯ = 2 1 ( 1 1 1 − 2 1 2 + 3 1 3 − 4 1 4 + − ⋯ ) = 2 1 ⋅ ln ( 1 + 1 ) = 2 1 ln 2 = ln 2 ≈ 0 . 3 4 6 6 . Thus x is a rational multiple of π (option 4) and y is the natural logarithm of the square root of a rational number (option 2). The solution is 4 2 .
Using complex number z = x + y i . we note that z 1 = 1 , z 2 = 1 + 2 i , z 3 = 1 + 2 i + 3 i 2 , implies that:
z ∞ = 1 + 2 i + 3 i 2 + 4 i 3 + ⋯ = i 1 ( i + 2 i 2 + 3 i 3 + 4 i 4 + ⋯ ) = − i 1 ln ( 1 − i ) = i ln ( 2 ( 2 1 − 2 i ) ) = i ln ( 2 e − 4 π i ) = i ( ln 2 − 4 π i ) = 4 π + i ln 2 Note that − ln ( 1 − x ) = k = 1 ∑ ∞ k x k By Euler’s formula e θ = cos θ + i sin θ
⟹ x = 4 π code: 4; y = ln 2 code: 2. Therefore, the answer is 4 2 .