Rectangular Symmetry

Geometry Level 2

True or false?

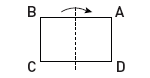
Every straight line that cuts a rectangle in half is an axis of reflectional symmetry for the rectangle.

False True

View wiki
Clara Blackstone by Clara Blackstone , 32, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Clara Blackstone
Oct 16, 2015

False -- only the horizontal and vertical cuts are axes of reflection symmetry. A diagonal cut has rotational symmetry, but try reflecting on it it and you don't get a rectangle, you get a kite!

3 Helpful 0 Interesting 1 Brilliant 0 Confused

"A diagonal cut has rotational symmetry, but try reflecting on it and you don't get a rectangle, you get a kite!' I did try, and I got another (congruent) rectangle, not a kite ;)

Otto Bretscher - 5 years, 8 months ago

Log in to reply

Thanks, I clarified the problem to read "axis of reflectional symmetry" instead of just axis of symmetry. That's almost certainly more easily understandable (so thanks for pointing out the need to clarify!), but it also seems redundant to me. Mainly, reflection is the only kind of symmetry specified by a fixed axis. (Glide reflections have an axis, but it gets translated, and that's not a relevant symmetry in this problem in any case).

My thought writing the problem was that rotational symmetry doesn't have a fixed axis, it's specified by a point and a degree of rotation, and only that one point is fixed, everything else moves. Most lines move entirely during a rotation and each line through the point of rotational symmetry gets flipped around if the angle of the rotation is 180 degrees. So there's no 'special' axis, even for a 180-degree rotation. Although... it is frequently really useful to think of a 180 rotation as two sequential reflections over perpendicular axes that intersect at the fixed point of the rotation. :D

Thanks for the feedback though, I think the problem statement is much clearer now & it's therefore a better problem!

Clara Blackstone - 5 years, 7 months ago

Log in to reply

No, Otto's point is that he is considering a square (in which a diagonal is also a reflection axis; you need to pick a different line).

Ivan Koswara - 5 years, 7 months ago

Thank you! My point remains, though, that reflecting a rectangle across a diagonal still gives you a (different but congruent) rectangle, not a kite.

Otto Bretscher - 5 years, 7 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...