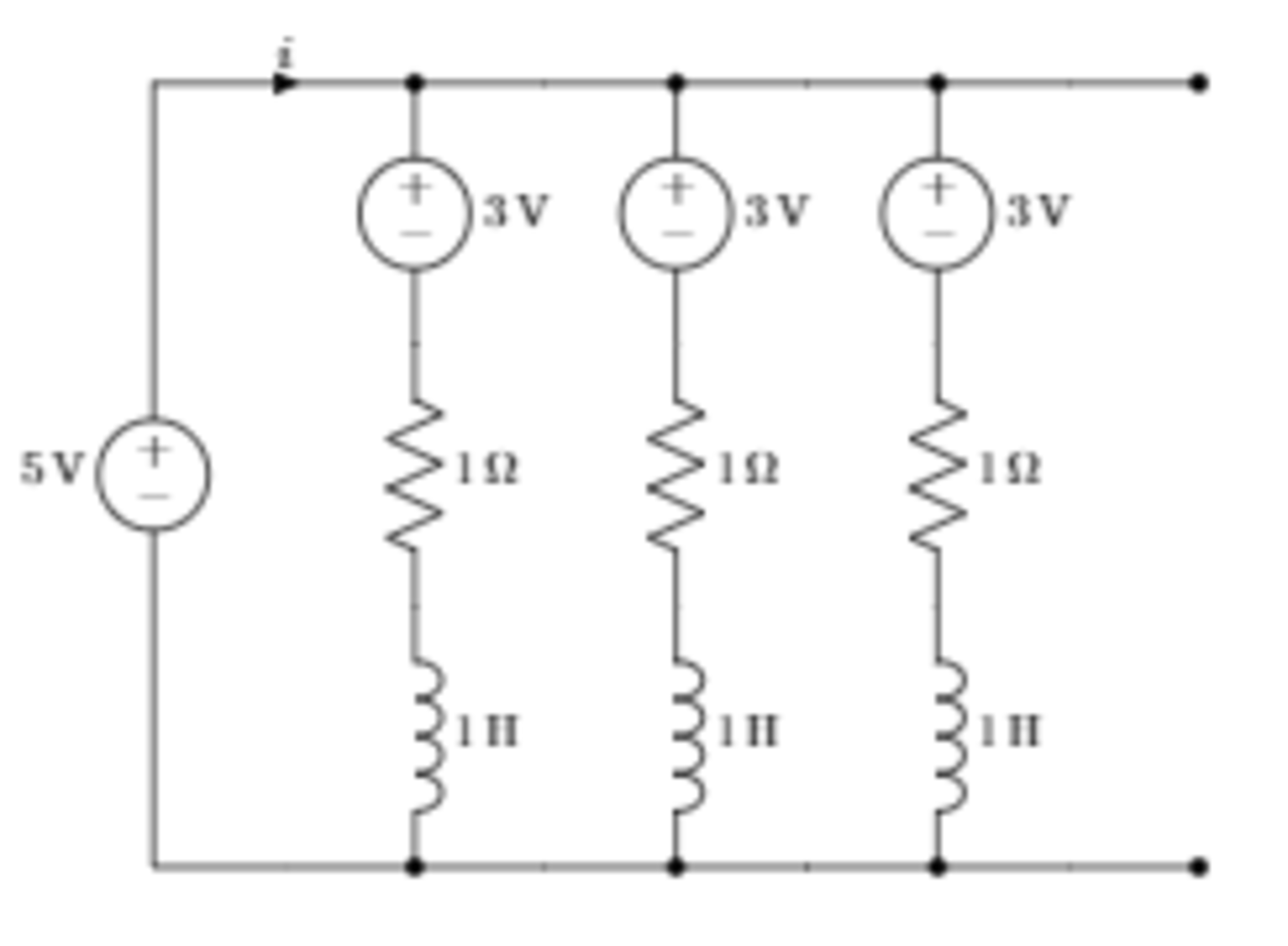
Recurring RL branch.

Electricity and Magnetism Level 3

Consider the following RL circuit, in which the RL branches are replicated n n times. (In the picture, there are 3.) The circuit has been in this state for a long time, so it has reached steady state at t = 0 − t = 0^- . Let i ( t , n ) i(t,n) be the current through the 5 V 5\rm V source. If all of the inductors have been de-energized at t = 0 t = 0 , calculate the integral I = ∑ n = 1 ∞ ∫ 0 7 i ( t , n ) d t I = \displaystyle \sum_{n = 1}^{\infty} \int_{0}^{7} i(t,n) dt If I = A + A B e C I= A + \frac{A}{B}e^C , enter A + B + C A + B +C .

Assume that ∑ n = 1 ∞ n = − 1 12 \displaystyle \sum_{n=1}^{\infty} n = \frac{-1}{12} .


The answer is -2.

Charley Shi by Charley Shi , 19, New Zealand

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Karan Chatrath
May 2, 2021

The governing equation for current through each branch is:

I ˙ + I = 2 ; I ( 0 ) = 0 \dot{I} + I = 2 \ ; \ I(0)=0 e t I ˙ + e t I = 2 e t \mathrm{e}^{t}\dot{I} + \mathrm{e}^{t}I = 2\mathrm{e}^{t} d d t ( e t I ) = 2 e t \frac{d}{dt}\left(\mathrm{e}^{t}I\right) = 2 \mathrm{e}^{t} ⟹ e t I = 2 e t + C \implies \mathrm{e}^{t}I = 2\mathrm{e}^{t} + C

Applying initial cindition leads to C = − 2 C = -2 . The current through each branch of the circuit as a function of time is:

I ( t ) = 2 ( 1 − e − t ) I(t) = 2(1 - \mathrm{e}^{-t})

The current through the 5 V 5 \ \mathrm{V} source is:

I ( n , t ) = 2 n ( 1 − e − t ) I(n,t) = 2n(1 - \mathrm{e}^{-t}) ∫ 0 7 I ( n , t ) d t = n ( 12 + 2 e − 7 ) \int_{0}^{7} I(n,t) \ dt = n\left(12 + 2\mathrm{e}^{-7}\right) Finally:

∑ n = 1 ∞ ∫ 0 7 I ( n , t ) d t = − 12 + 2 e − 7 12 = − 1 − e − 7 6 \sum_{n=1}^{\infty} \int_{0}^{7} I(n,t) \ dt = -\frac{12 + 2\mathrm{e}^{-7}}{12}= -1 -\frac{\mathrm{e}^{-7}}{6}

The answer evaluates to − 2 \boxed{-2} .

1 Helpful 1 Interesting 1 Brilliant 0 Confused

@Karan Chatrath Nice solution.
How are you.please provide me a anayltical solution of this problem.

Talulah Riley - 1 month, 1 week ago

Log in to reply

Since you have not shared an attempt like I have advised many times before, I am not sharing my solution. Instead, I can give you a few helpful hints.

Consider that rod 1 makes an angle θ 1 \theta_1 with the vertical and rod 2 makes an angle θ 2 \theta_2 with the vertical. Identify the forces acting on both rods. On rod 1:

  • Weight of the rod
  • X component of hinge force at O.
  • Y component of hinge force at O.
  • X component of hinge force at P.
  • Y component of hinge force at P.

On rod 2:

  • Weight of the rod
  • X component of hinge force at P - Equal and opposite to the hinge force exerted on rod 1
  • Y component of hinge force at P - Equal and opposite to the hinge force exerted on rod 1

Draw a free body diagram depicting these forces (2 known and 4 unknown components). Apply the laws of motion to find equations for accelerations for each rod along the X and Y directions. Find the net torque about the COM of each rod due to these forces. Doing this will give rise to 6 equations. Derive these equations yourself.

However, you have 10 unknown variables.

  • 4 hinge force components

  • a x 1 a_{x1}

  • a y 1 a_{y1}

  • a x 2 a_{x2}

  • a y 2 a_{y2}

  • θ ¨ 1 \ddot{\theta}_1

  • θ ¨ 1 \ddot{\theta}_1

You need 4 more equations. How do you obtain them? Think about it. Note that O O is the origin and the X axis is pointing horizontally to the right and Y axis is vertical upwards.

Karan Chatrath - 1 month, 1 week ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...