Recurring Styles 13 - Game of Inequalities!
a n + 1 = n a n + a n n , a 1 = 1
Let the sequence ⟨ a n ⟩ be defined as above for all positive integers n . Evaluate ⌊ a 2 0 1 5 ⌋
The answer is 44.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Does anyone have a math solution?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
|
Is there a mathematical method??? @Pi Han Goh @Brian Charlesworth ??
Log in to reply
I think yes, ⌊ a n ⌋ is closest integer value to n ... maybe?
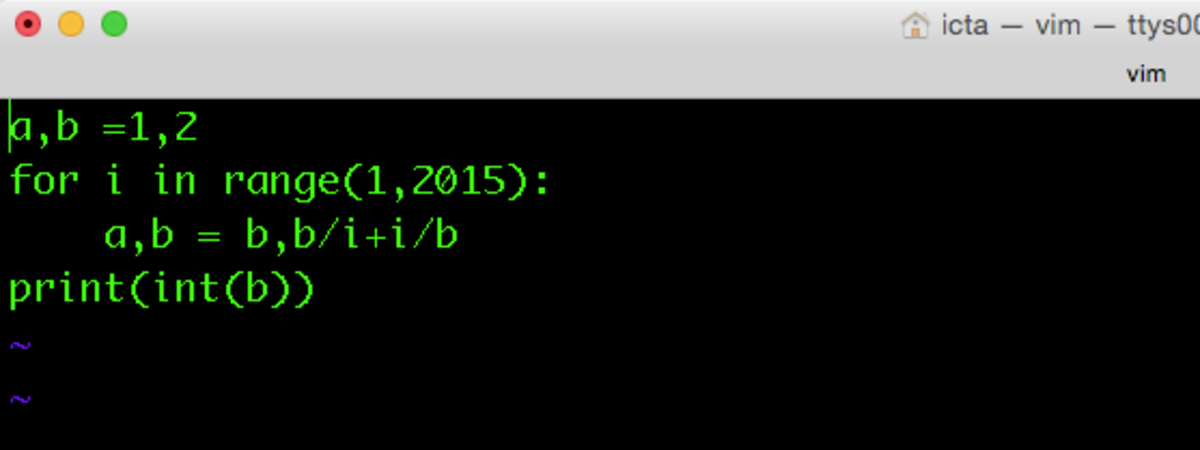
easy python3: