Recursion Warmup - Tower Numbers
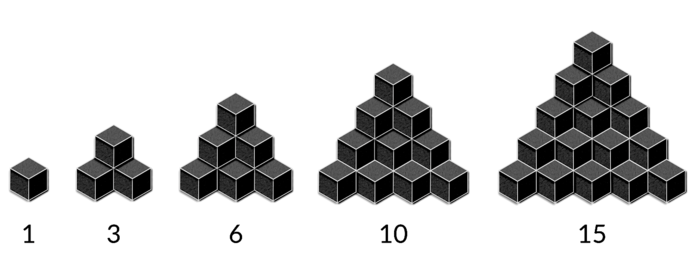 What is the next number in this sequence? (There are no hidden cubes.)
What is the next number in this sequence? (There are no hidden cubes.)
0 , 1 , 3 , 6 , 1 0 , 1 5 . . .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Those terms of the sequence (except the
0
) look like the 3rd pair of diagonals (moving inwards) of the pascal's triangle.
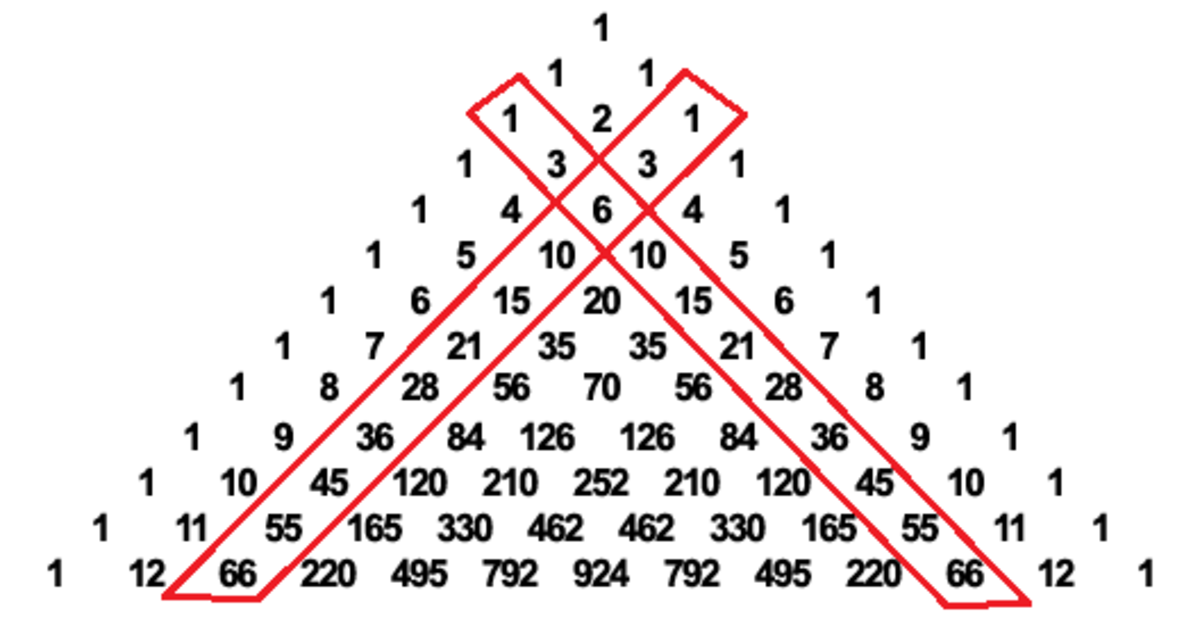 Those numbers are called triangular numbers and they can be generated by the formula:
T
n
=
(
2
n
+
1
)
Those numbers are called triangular numbers and they can be generated by the formula:
T
n
=
(
2
n
+
1
)
Hence for n = 6 we got: ( 2 n + 1 ) = 2 n ⋅ ( n + 1 ) = 2 6 ⋅ 7 = 2 1
The base of the shape are the key, Let's be n the number of cube in the base, then in the next "floor" would be n-1 cube and so recursively, then the function than represent the number of cube in the shape are ∑ i = 1 n i ; now from n=6 the answer are 21
1+2=3, 1+2+3=6,...,1+2+3+4+5+6=21.
n 1=1, n (i>1)=i^2-n_(i-1),i ⊂ N
This is the formation of triangles in the outside layer of a triangle, it means the blocks must increased by 1 in every layer. To the 5 t h row, the blocks are 1 5 + ( 1 × 5 ) + 1 = 2 1
1 5 is the 5 t h row, and 1 × 5 is the blocks increased each row times the row, plus 1 to get the sixth layer.