Recursive division is beautiful

Geometry Level 4

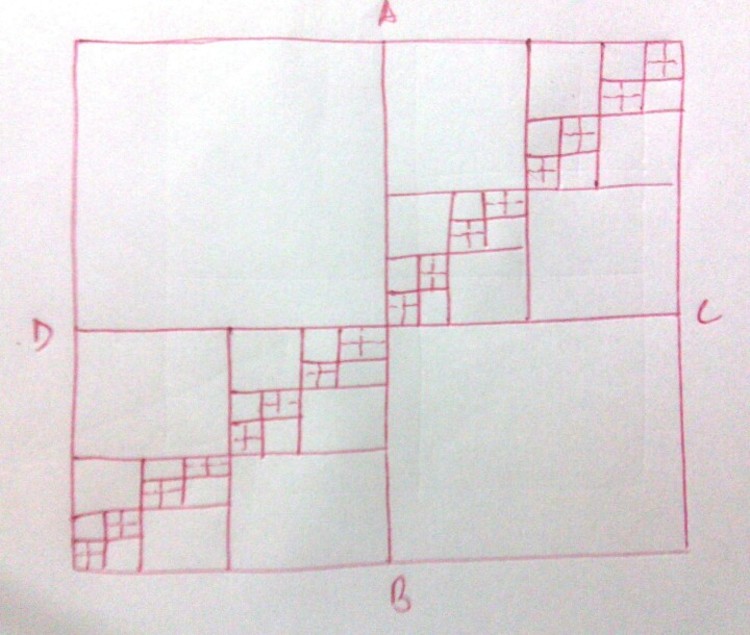As shown in figure is a square, if AB and CD represents the first division making 4 squares inside the biggest square, then calculate the total number of squares upto 10 divisions. The dotted line shows the pattern of division in the figure.

This problem is original.

The answer is 4093.

1 solution

Maggie Miller
Jul 19, 2015

Note that we are dividing twice as many squares into fourths in each division. We divide one square into fourths on the first division, so we divide $2^{n-1}$ squares into fourths on the $n$ -th division, creating $4\cdot 2^{n-1}=2^{n+1}$ new squares.

Therefore, after $n$ divisions, the total number of squares is $1+\displaystyle\sum_{k=0}^n2^{n+1}=1+4(2^n-1).$

Plugging in $n=10$ , we find that the answer is $\displaystyle 1+4(2^{10}-1)=\boxed{4093}$ .

Well your answer equals to 4092, the biggest square has also to be added. This is the only approach for this question.

Abhay Tiwari - 5 years, 10 months ago

No. of squares in 1st division = (4×1)
No. of squares in 2nd division = (4×1) + (4×2)
No. of squares in 3rd division = (4×1) + (4×2) + (4×4)
No. of squares in 4rth division = (4×1) + (4×2) + (4×4) + (4×8)

We see that in nth division the number of squares is given by $4 × \displaystyle \sum_{n=0}^{n} 2^{n-1}$

So, in 10th division, the number of squares will be $4 × \displaystyle \sum_{n=0}^{10} 2^{n-1}$
= $4 × 1023 = 4092$

But as mentioned, I forgot to add the biggest square, so the answer is ultimately $4092 + 1 = \boxed{4093}$

Ashish Menon - 5 years, 1 month ago

Haha wow yes, I mentally added the one but forgot to write it down! Thanks

Maggie Miller - 5 years, 10 months ago

Great problem, I forgot to add 1 but got 4092 with a different approach which I shall specify.

Ashish Menon - 5 years, 1 month ago

Recursive division is beautiful

The answer is 4093.

1 solution

0 pending reports