Red and blue nodes
Here is a triangular lattice of linear dimension 4, consisting of 16 unit equilateral triangles:
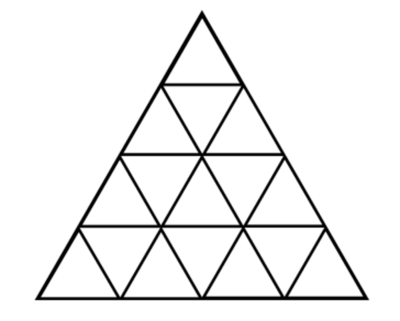
Suppose you mark each node with a red or blue circle. (There are 15 nodes in the figure above)
What is the largest dimension of a triangular lattice (constructed similarly to the one above in the shape of a triangle) you can color, such that no three corners of any of the equilateral triangles it contains of any size (with lines lying on the lattice lines) are colored the same color?
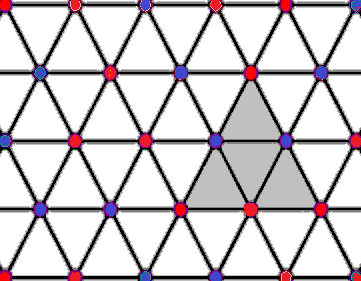
For example, the following would be illegal since the nodes on the corners of the triangle shaded grey are all red:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There is one in the diagram given, a 3 dimension triangle that contains the grey one on the right side, the one whose apex is the 4th point in the first row. I couldn't find any triangle higher than that.