Red area = yellow area
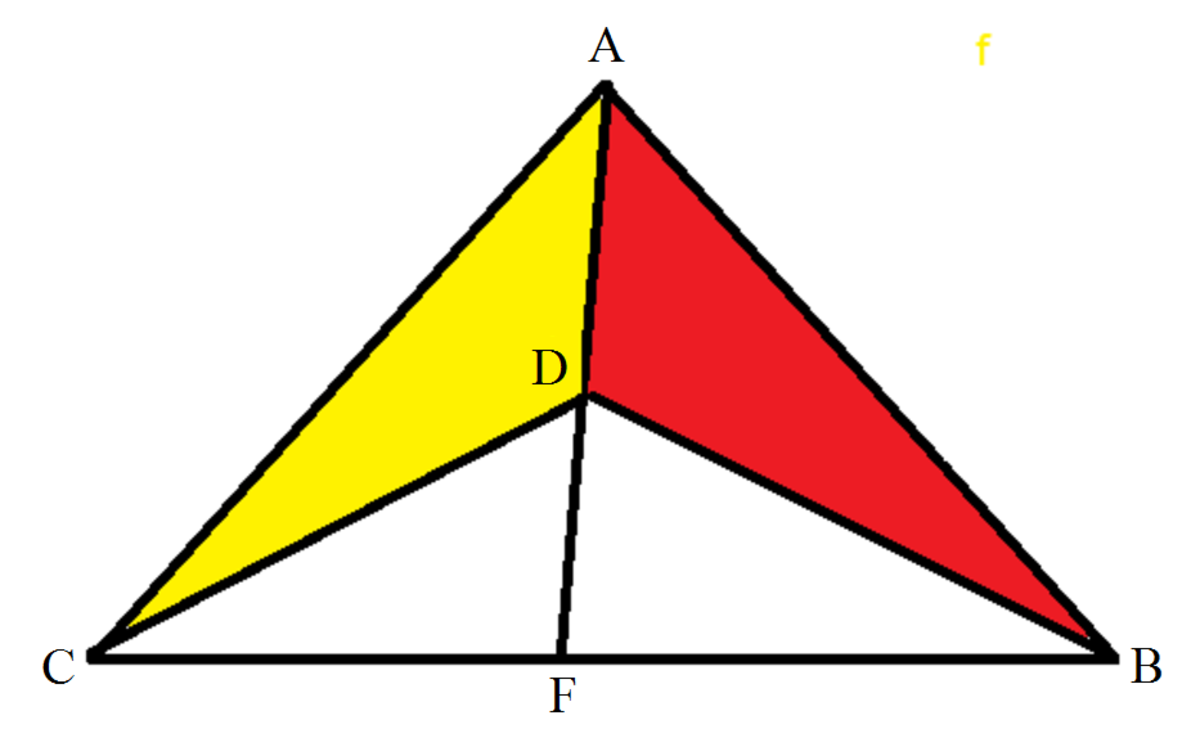
If the area shaded red is equal to the area shaded yellow, what is C F B F ?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
You're missing a good deal here. We're not told AD and CF are perpendicular. And they need not be.
Draw two lines parallel to A F , one passing through B and the other through C . Since yellow triangle and red triangle have the same area and the same base length, therefore they have the same height. This means that the two parallel lines through B and C are equidistant from A F . This means that any line such as C B cutting the two parallel lines is bisected by A F . That is B F = C F and C F B F = 1 .
Let ∠ B A F = α and ∠ A F B = β . Then, since the area of the triangles △ A B D and △ A C D are equal, therefore ∣ A B ∣ sin α = ∣ A C ∣ sin ( A − α ) , where A = ∠ B A C . Applying Sine Rule to △ A B F we get ∣ B F ∣ = sin β ∣ A B ∣ sin α . Applying Sine Rule to △ A C F we get ∣ C F ∣ = sin β ∣ A C ∣ sin ( A − α ) . So ∣ B F ∣ ∣ C F ∣ = ∣ A B ∣ sin α ∣ A C ∣ sin ( A − α ) = 1
When we draw all the three medians of any triangle, then the triangle gets divided into 6 smaller triangles .
And all these 6 smaller triangles are equal in area . You can watch it's proof on
https://www.khanacademy.org/math/geometry-home/triangle-properties/medians-centroids/v/medians-divide-into-smaller-triangles-of-equal-area
It is given that the area of the yellow portion is equal to the area of the red portion. And we can see that the yellow area is the sum of two smaller triangles. Similar is the red one. So according to this we can deduce that AF is one of the median .
Which means that CF=BF .
Hope this helps 🙂
Using convention that a d = distance from point a to point d .
Let g and h be the points on the line a f closest to points b and c , respectively.
The area of the yellow triangle is ( 1 / 2 ) ∗ a d ∗ b g . The area of the red triangle is ( 1 / 2 ) ∗ a d ∗ c h .
Since these quantities are equal, we know that the line a f is equidistant from points b and c , i.e. b g = c h .
Note that if either g = f or h = f , then the other must also equal f , and we have b f = c f .
Consider triangles △ b g f and △ c h f .
1) Both angles ∠ b g f and ∠ c h f are right angles by choice of g , h .
2) Angles ∠ b f g and ∠ c f h are vertical angles and thus are congruent.
3) Apply Side-Angle-Angle theorem: since two pairs of corresponding angles are congruent, and one pair of corresponding sides are congruent ( b f = c f ), the triangles are congruent.
And since they are congruent triangles, b f = c f .
Since they have the same areas,
(AD)(CF) = (AD)(BF)
BF/CF = 1