Red, Blue, Yellow, & Bleach

Probability Level 3

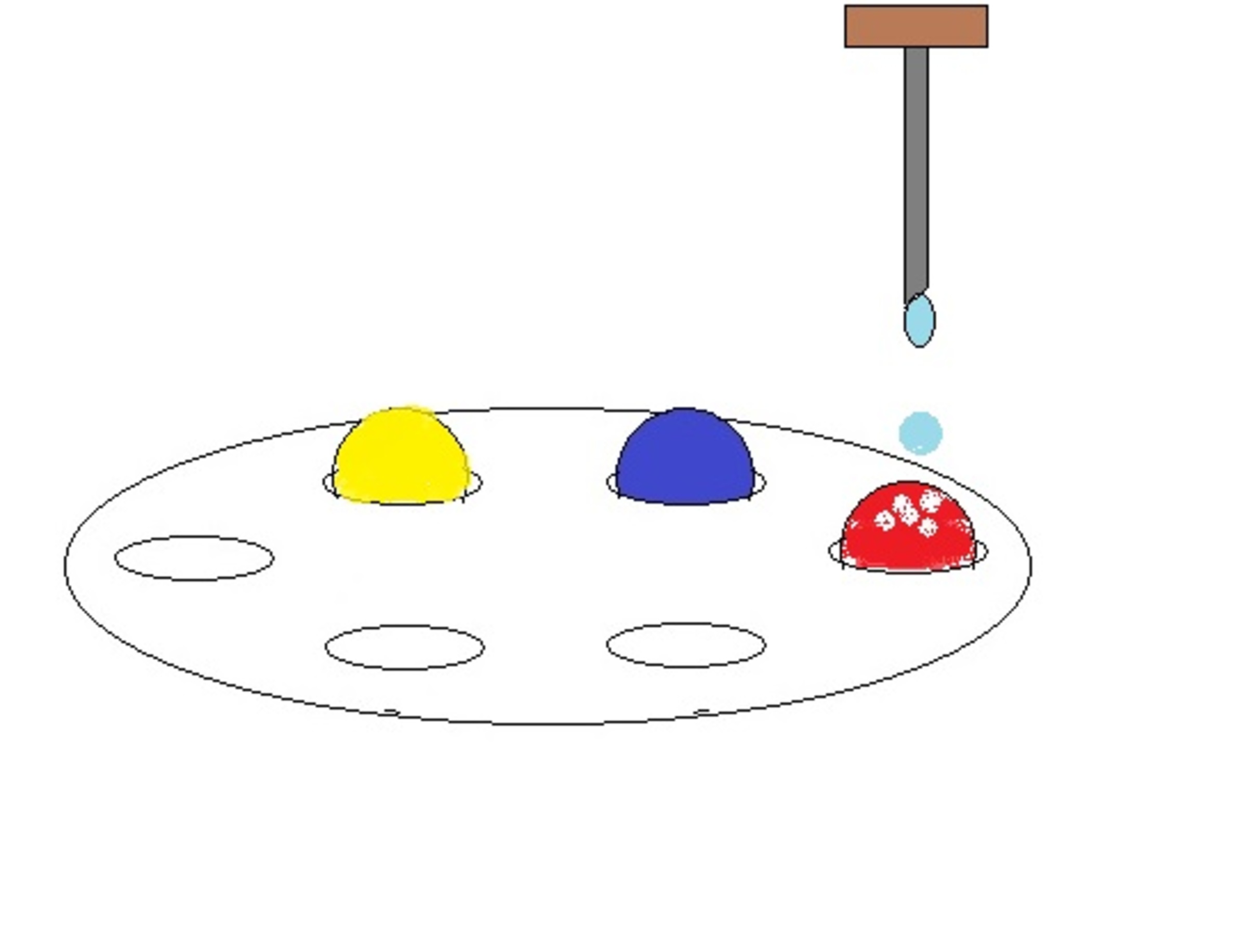
Three balls of the same size but different colors (red, blue, yellow) are placed randomly on the tray with 6 holes. Then the springer above will randomly pour down the bleach into 3 out of the 6 holes.

Once bleached, any color will turn white, and the chemical may hit 1 ball, 2 balls, 3 balls, or none at all.

How many sets of color balls are there in this scenario?

The answer is 8.

2 solutions

Colin Carmody
Apr 15, 2016

Each ball will either get hit, or it will not get hit. So each ball has two possible states, a 1/2 chance of each. There are three balls, so cube this, to get 1/8. One out of 8 possibilities will happen, so the answer is 8.

Worranat Pakornrat
Apr 15, 2016

Let $R$ = red, $B$ = blue, $Y$ = yellow, and $W$ = white.

If no balls are bleached, the combination is $\binom{3}{0} = 1$ : (R, B, Y).

If 1 ball is bleached, the combination is $\binom{3}{1} = 3$ : (W, B, Y), (R, W, Y), (R, B, W).

If 2 balls are bleached, the combination is $\binom{3}{2} = 3$ : (R, W, W), (W, B, W), (W, W, Y).

If 3 balls are bleached, the combination is $\binom{3}{3} = 1$ : (W, W, W).

Thus, totally there are $\boxed{8}$ sets of the colored balls.

Red, Blue, Yellow, & Bleach

The answer is 8.

2 solutions

0 pending reports