Red-carded

Probability Level 2

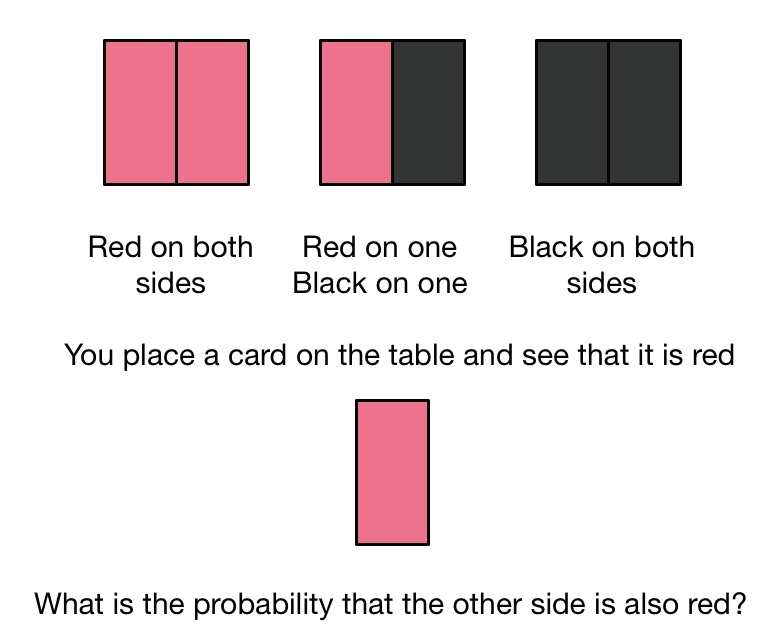
There are three cards on a table. One of them is black on both sides, one of them is black on one side and red on the other, and one of them is red on both sides.

One of these three cards is selected at random and placed on a second table with a side randomly chosen to face up. The side facing upward is red.

What is the probability that the side facing the table is also red?

1 3 \frac13 1 2 \frac12 2 3 \frac23 Cannot be determined from given information

View wiki
Denton Young by Denton Young , 47, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Denton Young
Mar 30, 2016

Relevant wiki: Probability - By Complement

The cards on the table have three red sides (two from the card red on both sides, one from the red-black card).

The only way the selected card could not have its other side be red is if the side facing upward is the single red side from the red-black card. Since there are three red sides, and the selection was random, the chances of this are 1/3. So the chance the other side IS red is 1 - 1/3 = 2/3.

11 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Good analysis of the probabilities.

This would be true BEFORE a card is put on the table... AFTER a selection is made, there are only two possible outcomes: either the other side of the card is red or it is black. The third state of black/black becomes a forbidden one once the card is put on the table, red face up!!!!

A Solver - 5 years, 1 month ago

Log in to reply

The argument in Denton's Solution is that the third state of black-black has already been excluded. If you had seen a black then the probability of having drawn a red-red drops to 0.

By knowing that you are left with the red-black card and the red-red card your options have been limited. Of the cards remaining you know that there are three red sides and one black side. You also know you are looking at one of the three red sides.

In the scenario that you drew the red-black card, then you must have drawn the only red side that has black on the other. Given that there are three red sides and the draw was truly random then the probability of drawing this red side was 1/3. In any other draw, for you to see a red, the red-red card must have been drawn. Thus the probability of drawing a red-red card is 1-(1/3) = 2/3.

Ross Sheddan - 5 years, 1 month ago

Nope, you understood it wrong. Think it as the the problem with identical redballs. The first card (the one with both halves red) actually forms the third case and not the both side black one. Either of the two sides of that red card could be up therefore there are three possibilities instead of two, I also got it wrong xD. Never assume identical things unless given in a probability question ;)

aneesh kejariwal - 5 years, 1 month ago

What does any of that have to do with the price of tea in China?

Denton Young - 5 years, 1 month ago

Log in to reply

you'd be surprised, almost as surprised as I am when I saw the price of tea in china

Liam Scarstrike - 5 years, 1 month ago

The sides of the cards are not separate entities that can be selected by themselves. They are selected in pairs, that is to say on a card. Once you see the red side you know the card isn't the black-black card. That leaves two possibilities: red-red and red-black, which are now equally likely. So there is a 50% chance the card is red-red and a 50% chance it is red-black.

Brandon Stocks - 5 years, 1 month ago

I got it wrong too and had to draw it out.

Each of the three cards can be in one of two states:

Card:.....1........2.......3

Front... R R | R B | B B

Back... R R | B R | B B

Once the random card is shown to have a Red front, there are only three possible states in total:

Card:.....1......2

Front... R R | R

Back... R R | B

With equal probability, it could be any of those three states. There is a 2/3 probability that the back is Red.

Steve Riese - 5 years, 1 month ago

In the bottom, we can have red, red or black. Therefore the chances of having a red in the bottom is 2/3.

Mostafa Lazaret - 5 years, 1 month ago

Do not take the card with black on both sides into consideration since we know it is definitely not that one. That leaves us with the red on both sides and the red on one side. There are 3 red sides in total (2 from the first card and 1 from the second card). On 2 of these sides, the opposite is also read so we have 2/3 as our final probability.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...