Red Light Green Light

Logic Level 2

You have an unlimited pile of bars which are slightly arrow-shaped and have four lights in a row. When on, the lights can either be green or red, but currently all the lights are off.

You are then given two bars that are turned on. On one bar the first two lights are green but the last two lights are red, and on the other bar the first and third lights are green but the second and fourth lights are red.

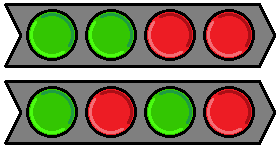
You may then do the following steps in any order and as many times as you like:

If you touch any bar that is on to any bar that is off, the bar that is off will turn on with the same red and green light sequence as the bar that is on (where both bars are pointing in the same direction).
If you shake any bar that is on, all the lights will switch colors (all the green lights will turn red and all the red lights will turn green).
If you touch any two bars that are on to any bar that is off, the bar that is off will turn on, and its light will turn green if both corresponding lights of the other two bars are also green (where both bars are pointing in the same direction), but will otherwise turn red.

Starting with the two given bars and using the above given steps, is it possible to make all 16 possible green and red color combination of the four lights on each bar?

No Yes

1 solution

David Vreken
Nov 19, 2018

The bars are similar to columns of a logical truth table , where the green light is true and the red light is false, where the second step is negation ( $\sim p$ ) and the third step is conjunction ( $p \wedge q$ ). Therefore, we are trying to see if we can obtain all $16$ possible true and false combinations with just $p$ , $q$ , negation ( $\sim$ ), and conjuction ( $\wedge$ ).

Below is a table of all $16$ possible true and false combinations. Starting with the original two lighted bars, which we will call $p$ and $q$ respectively, we have $TTFF$ and $TFTF$ . By Step $3$ , touching these two bars to a bar that is off will give us $TFFF$ , the logical equivalent to $p \wedge q$ .

Cloning these bars by Step $1$ and negating them by Step $2$ , we get $\sim p$ (which is $FFTT$ ), $\sim q$ (which is $FTFT$ ) and $\sim (p \wedge q)$ (which is $FTTT$ ).

Using different variations of $p$ , $\sim p$ , $q$ , and $\sim q$ with conjunction, we have $p \wedge \sim p$ (which is $FFFF$ ), $p \wedge \sim q$ (which is $FTFF$ ), $\sim p \wedge q$ (which is $FFTF$ ), and $\sim p \wedge \sim q$ (which is $FFFT$ ), and their negations $\sim (p \wedge \sim p)$ (which is $TTTT$ ), $\sim (p \wedge \sim q)$ (which is $TFTT$ ), $\sim (\sim p \wedge q)$ (which is $TTFT$ ), and $\sim (\sim p \wedge \sim q)$ (which is $TTTF$ ).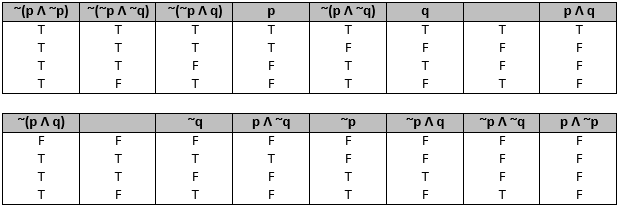

This leaves two left, which can be obtained by $\sim (\sim p \wedge q) \wedge \sim (p \wedge \sim q)$ (which is $TFFT$ ) and its negation $\sim (\sim (\sim p \wedge q) \wedge \sim (p \wedge \sim q))$ (which is $FTTF$ ).

Therefore, it is possible to make all $16$ possible green and red color combination of the four lights on each bar.

Nice explanation, David!

I was wondering how you were able to make such cool looking tables. Then I realized they are images! :)

Geoff Pilling - 2 years, 6 months ago

Thanks! I was going to do the tables in Latex but then I decided it would be easier for me to do them in Microsoft Word and screenshot the images.

David Vreken - 2 years, 6 months ago

I use google drawings and they had tables to add in my images for my problems @sucheng zhu

I changed my name. - 2 years, 1 month ago

I knew I was able to but I did not need to do all these tables in my head I only took a pencil a red and green crayon and redrew it until I got it :)

Helena Blachut - 2 years, 6 months ago

Red Light Green Light

1 solution

0 pending reports