Red vs. Blue: The Hexagon Edition

The red triangle can be cut and rotated as follows, preserving its area:

The blue triangle has the same base but twice the height as the red triangle, so its area is twice as big.

The ratio of the red triangle to the blue triangle is therefore $\frac{1}{2}$ , so $A = 1$ and $B = 2$ , and $B - A = 2 - 1 = \boxed{1}$ .

There's a more efficient visual way to answer this, but I wanted to use some Precalculus!

Let $s$ be the side length of the regular hexagon and $h$ be the vertical height of both the red and blue triangle.

Because each interior angle of a regular hexagon is $120^{o}$ , you can use the Law of Cosines with the red triangle to solve for $h$ in terms of $s$ .

$h^{2}=s^{2}+s^{2}-2s^{2}\cos 120^{o}$

$h=s\sqrt{3}$

Using $A=\frac{1}{2}ab\sin C$ for the red triangle, I found $A=\frac{1}{2}s^{2}\sin 120^{o}=\frac{\sqrt{3}}{4}s^{2}$ . Using $A=\frac{1}{2}bh$ for the blue triangle, I found $A=\frac{1}{2}s\cdot s\sqrt{3}=\frac{3}{2}s^{2}$ .

The blue triangle's area is twice that of the red triangle's area, so the ratio of red to blue is $\frac{1}{2}$ . Since $A=1$ and $B=2$ , $B-A=\fbox{1}$ .

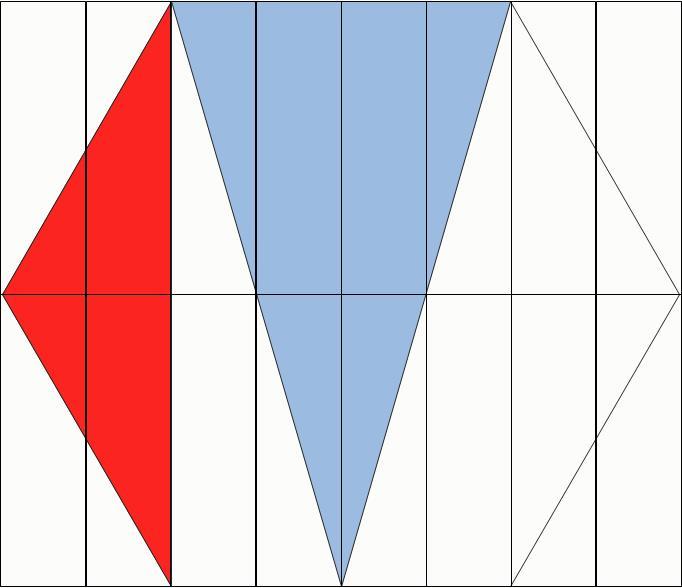
From the picture below:

Lets assume that each small rectangle has an area equal to $R$

Red area = $0.5 * 4 * R$ $= 2 R$

Blue area = $0.5 * 8 * R$ $= 4 R$

Red to Blue area = $\frac{2 R}{4 R}$

$\frac{A}{B}$ = $\frac{1}{2}$

$B - A = \boxed{1}$