Reflect point

It is easy to compute that $\angle APC = 135^\circ$ . Since this is half of reflex angle $\angle ABC$ , which is $270^\circ$ , $P$ lies on the circle centered at $B$ with radius $AB$ . Then $\angle PBA = 2 \angle PCA = 40^\circ$ .

Let $\angle {PBA}=α$ . We can easily see that $\angle {CAP}=\angle {CAD}-\angle {PAD}=45\degree-20\degree=25\degree$

Similarly, $\angle {ACP}=20\degree$

So, $\angle {BAP}=45\degree+25\degree=70\degree$

$\angle {BCP}=45\degree+20\degree=65\degree$ .

Applying sine rule to $\triangle {BAP}$ , we can write

$\dfrac {|\overline {AB}|}{|\overline {BP}|}=\dfrac {\sin (70\degree+α)}{\sin 70\degree}$

Applying sine rule to $\triangle {BCP}$ ,

$\dfrac {|\overline {BC}|}{|\overline {BP}|}=\dfrac {\sin (25\degree+α)}{\sin 65\degree}$

Since $|\overline {AB}|=|\overline {BC},$ therefore

$\sin 65\degree\sin (70\degree+α)=\sin 70\degree\sin (25\degree+α)$

$\implies \tan α=\dfrac {\sin 70\degree(\sin 65\degree-\sin 25\degree)}{\sin 70\degree\cos 25\degree-\sin 65\degree\cos 70\degree}$

$\implies α=\boxed {40\degree}$ .

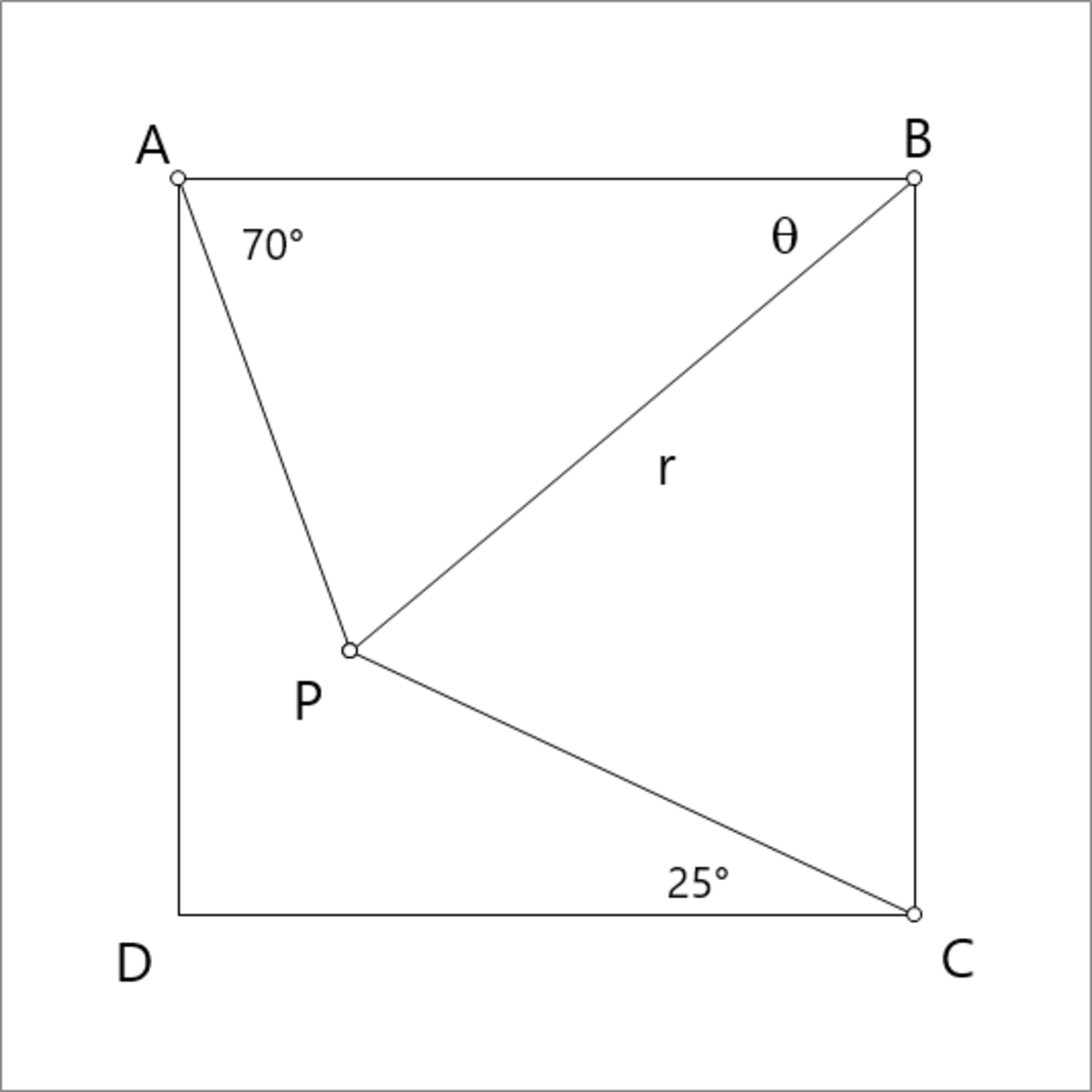
Let the side length of the square be $1$ , so that $A = (0, 1), B = (1,1), C= (1, 0), D = (0,0)$ , and let $\theta = \angle PBA$ , and let $r = \overline{PB}$

The coordinates of $P$ are:

$P = ( 1 - r \cos \theta, 1 - r \sin \theta)$

$CP$ makes an angle of $25^{\circ}$ with the horizontal, this translates into,

$\dfrac{1 - r \sin \theta} {- r \cos \theta } = - \tan 25^{\circ}$

and

$AP$ makes an angle of $70^{\circ}$ with the horizontal, this translates into,

$\dfrac{ -r \sin \theta } { 1 - r \cos \theta } = - \tan 70^{\circ}$

These two equations yield,

$r ( \sin \theta + \tan 70^{\circ} \cos \theta ) = \tan 70^{\circ}$

and,

$r ( \tan 25^{\circ} \cos \theta + \sin \theta) = 1$

dividing $r$ out,

$\sin \theta + \tan 70^{\circ} \cos \theta = \tan 70^{\circ} ( \tan 25^{\circ} \cos \theta + \sin \theta)$

dividing by $\cos \theta$ ,

$\tan \theta = \dfrac{ \tan 70^{\circ} ( \tan 25^{\circ} - 1) }{1 - \tan 70^{\circ}} = 0.839099631177280...$

From which $\theta = \boxed{40^{\circ}}$