Reflection across a circular arc
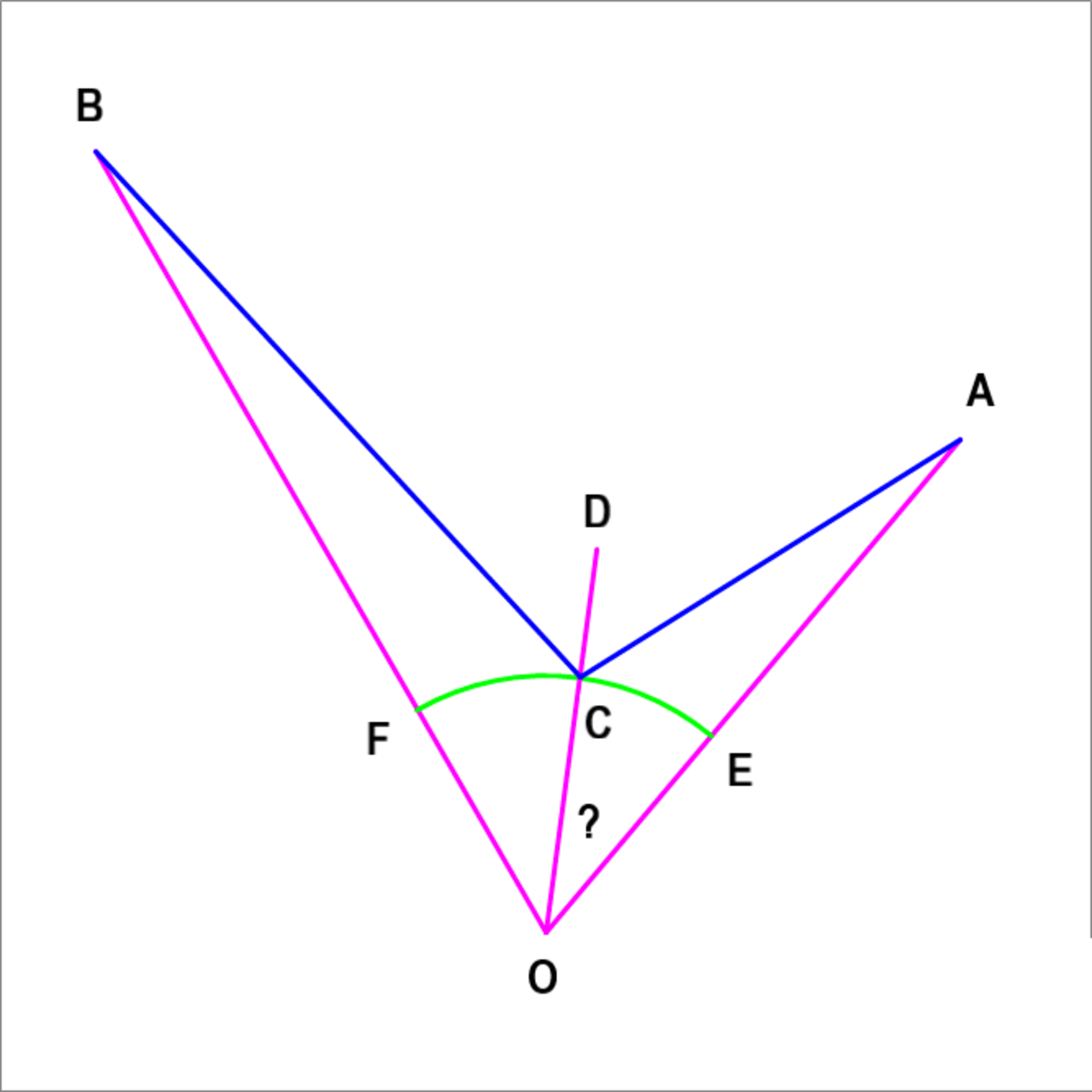
A circular arc E F (shown in green) makes a central angle of ∠ E O F = 7 0 ∘ . O A is a line segment containing point E , and of length 5 , and O B is a line segment containing point F , and of length 7 , while the radius of the green arc is 2 . We want to find point C on the arc such that a ray A C incident on the arc reflects into ray C B passing through point B . That is to say ∠ A C D = ∠ B C D . Find ∠ C O A in degrees.
The answer is 32.38.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Applying Sine Rule to the △ ′ s A O C and B O D we get 4 9 0 0 s i n 4 α − 1 3 1 5 . 5 6 9 7 s i n 3 α − 4 5 0 8 . 2 3 4 3 s i n 2 α + 3 4 2 . 8 1 8 9 s i n α + 9 0 8 . 6 2 9 9 = 0 where α is the required angle. From this we get the value of s i n α in the given region to be equal to 3 2 . 3 8 4 6
Constants:
θ E O F = 7 0 ∘ R = 2 A x = 5 A y = 0 B x = 7 cos θ E O F B y = 7 sin θ E O F θ = ∠ C O A
Coordinates of point C :
C x = R cos θ C y = R sin θ
Incident vector from A to C :
v x = C x − A x v y = C y − A y
Normal and tangent vectors to circle:
N x = cos θ N y = sin θ T x = − N y T y = N x
Express v in terms of the normal and tangent vectors:
v x = α N x + β T x v y = α N y + β T y
Solve the system for ( α , β ) and construct the reflected vector v 2 :
v 2 x = − α N x + β T x v 2 y = − α N y + β T y
Equation of line O B :
y = m O B x
Trace the reflected ray from point C until it intersects line O B . Determine the travel distance until intersection.
C y + γ v 2 y = m O B ( C x + γ v 2 x ) γ = v 2 y − m O B v 2 x m O B C x − C y
Intersection point:
x i = C x + γ v 2 x y i = C y + γ v 2 y
Sweep the parameter θ and store the value of θ for which the following is true.
x i = B x y i = B y
This results in θ ≈ 3 2 . 3 8 ∘
L e t ∠ C O A = X . ∠ A C D = ∠ B C D , s o ∠ A C O = ∠ B C O = s a y Y . A p p l y i n g C o s R u l e t o Δ s A O C a n d B O C , A C 2 = 2 5 + 4 − 2 ∗ 5 ∗ 2 ∗ C o s X . . . . . . . . . . ( 1 ) B C 2 = 4 9 + 4 − 2 ∗ 7 ∗ 2 ∗ C o s ( 7 0 − X ) . . . . . . ( 2 ) A p p l y i n g S i n R u l e t o Δ s A O C a n d B O C , A C = 5 ∗ S i n X / S i n Y . . . . . . . . . . ( 3 ) B C = 7 ∗ S i n ( 7 0 − X ) / S i n Y . . . . . . . . . . ( 4 ) S u b t r a c t i n g S i n Y o f ( 2 ) a n d ( 4 ) f r o m S i n Y o f ( 1 ) a n d ( 3 ) , ( 5 ∗ S i n X ) 2 / ( 2 9 − 2 ∗ 5 ∗ 2 ∗ C o s X ) − ( 7 ∗ S i n ( 7 0 − X ) 2 / ( 5 1 − 2 ∗ 7 ∗ 2 ∗ C o s ( 7 0 − X ) ) = 0 S o l v i n g t h r o u g h K e i s a n O n l i n e C a l c u l a t o r X = 2 0 t o 6 0 , a n d r e f i n i n g , w e g e t ∠ C O A = 3 2 . 3 8 6 7 2 .
Let ϕ = ∠ E O F = 7 0 ∘ , and let θ = ∠ C O A . Also, let Ψ = ∠ O C A = ∠ O C B (because ∠ A C D = ∠ B C D ). Further, let a = O A , b = O B , r = O C
Using the Law of Sines in △ A O C , we obtain,
a sin Ψ = r sin ( π − θ − Ψ ) = r sin ( Ψ + θ )
Similarly, using the Law of Sines in △ B O C , we obtain,
b sin Ψ = r sin ( Ψ + ϕ − θ )
After some simple manipulation, the above two equations can be solved for tan Ψ , and from the first equation we obtain,
tan Ψ = r − a cos θ a sin θ
Similarly, the second equation yields,
tan Ψ = r − b cos ( ϕ − θ ) b sin ( ϕ − θ )
Equating the two expressions and cross multiplying, gives,
a sin θ ( r − b cos ( ϕ − θ ) ) = b sin ( ϕ − θ ) ( r − a cos θ )
Expanding cos ( ϕ − θ ) and sin ( ϕ − θ ) , the above equation becomes,
a sin θ ( r − b cos ϕ cos θ − b sin ϕ sin θ ) = b ( sin ϕ cos θ − cos ϕ sin θ ) ( r − a cos θ )
Muliplying the expressions out yields,
a r sin θ − a b cos ϕ sin θ cos θ − a b sin ϕ sin 2 θ = b r sin ϕ cos θ − b r cos ϕ sin θ − a b sin ϕ cos 2 θ + a b cos ϕ sin θ cos θ
Collecting terms, and using the identities cos 2 θ = cos 2 θ − sin 2 θ and sin 2 θ = 2 sin θ cos θ , we arrive at,
( b r sin ϕ ) cos θ + ( − a r − b r cos ϕ ) sin θ + ( − a b sin ϕ ) cos 2 θ + ( a b cos ϕ ) sin 2 θ = 0
To solve this equation, the reader is referred to the results of this problem or, one can find the solution by a numerical root-finding algorithm (e.g. Newton's method).
The solution is θ = 0 . 5 6 5 2 5 5 = 3 2 . 3 8 ∘
Let O ( 0 , 0 ) be the origin of the x y -plan, A ( 5 , 0 ) , and B ( 7 cos 7 0 ∘ , 7 sin 7 0 ∘ ) . Let the angle to be found ∠ C O A = θ . Then C ( 2 cos θ , 2 sin θ ) . From
∠ A C D ∠ C O A + ∠ C A O θ + tan − 1 ( 5 − 2 cos θ 2 sin θ ) = ∠ B C D = ∠ B C E − ∠ D C E = tan − 1 ( 7 cos 7 0 ∘ − 2 cos θ 7 sin 7 0 ∘ − 2 sin θ ) − θ where C E ∣ ∣ O A Note that ∠ D C E = ∠ C O A = θ
Solving the above numerically, we have θ ≈ 3 2 . 3 8 6 7 .