Reflection Box

Geometry Level 3

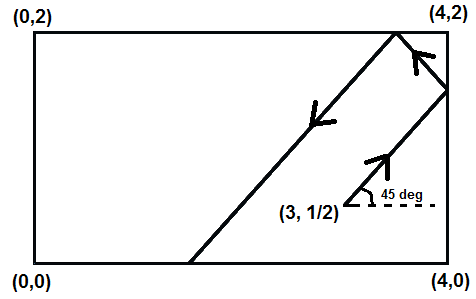
A beam of light is emitted within a rectangular box from point $(x,y) = (3,\frac{1}{2})$ at an angle of $45^{\circ}$ with respect to the horizontal. The coordinates of the four box corners are $(0,0),(4,0),(4,2),$ and $(0,2)$ , as shown in the figure.

The beam of light reflects off of the sides of the box such that the horizontal velocity is reversed when the beam strikes a vertical side, and the vertical velocity is reversed when the beam strikes a horizontal side.

Determine the $x$ coordinate of the location at which the beam first strikes the bottom side $(y=0)$ .

The answer is 1.5.

1 solution

Steven Chase
Aug 5, 2016

The key is that the absolute size of a change in $x$ is always going to be the same as the absolute size of the change in $y$ . But the relative signs may be the same or opposite, depending on the pattern of reflections.

Step 1) $x$ and $y$ velocities same: $x$ goes from $3$ to $4$ ( a change of $1$ ). $y$ goes from $\frac{1}{2}$ to $\frac{3}{2}$ ( a change of $1$ )

Step 2) $x$ and $y$ velocities opposite: $y$ goes from $\frac{3}{2}$ to $2$ ( a change of $\frac{1}{2}$ ). $x$ goes from 4 to $\frac{7}{2}$ ( a change of $\frac{-1}{2}$ )

Step 3) $x$ and $y$ velocities same: $y$ goes from $2$ to $0$ ( a change of $-2$ ). $x$ goes from $\frac{7}{2}$ to $\frac{3}{2}$ ( a change of $-2$ )

Reflection Box

The answer is 1.5.

1 solution

0 pending reports